Models with Categorical Variables

class: center, middle

![:scale 70%](./images/anova/cat-egorical.jpg)

## Models with Categorical Variables

---
# So, We've Done this Linear Deliciousness
`$$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$$`
`$$\epsilon_i \sim \mathcal{N}(0, \sigma)$$`

---
# And We've Seen Many Predictors
`$$y_i = \beta_0 + \sum^K_{j=1}\beta_j x_{ij} + \epsilon_i$$`

---

# What if our X Variable Is Categorical?
### Comparing Two Means

--
`$$mass_i = \beta_0 + \beta_1 sex_i + \epsilon_i$$`

---

# What if it Has Many Levels
### Comparing Many Means

--
`$$mass_i =  \beta_1 adelie_i + \beta_2 chinstrap_i + \beta_3 gentoo_i + \epsilon_i$$`

---
# Different Types of Categories?
### Comparing Many Means in Many categories

<img src="categorical_predictors_files/figure-html/unnamed-chunk-3-1.png" style="display: block; margin: auto;" />
--
`$$mass_i =  \beta_1 adelie_i + \beta_2 chinstrap_i + \beta_3 gentoo_i + \beta_4 male_i + \epsilon_i$$`

---
class:center

![](images/categorical_lm/corporate_categorical_lm.jpg)

---

# Dummy Codding for Dummy Models

1. The Categorical as Continuous

2. Many Levels of One Category

3. Interpretation of Categorical Results.

4. Querying Your Model to Compare Groups

---

# We Know the Linear Model
.large[
`$$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$$`
  
`$$\epsilon_i \sim N(0, \sigma)$$`
]

But, what if `$x_i$` was just 0,1?

---
# Consider Comparing Two Means
#### Consider the Horned Lizard 
.center[
![:scale 50%](images/09/horned_lizard.jpg)
]

Horns prevent these lizards from being eaten by birds. Are horn lengths different between living and dead lizards, indicating selection pressure?

---
class: center, middle
background-image: url("./images/09/gosset.jpg")
background-position: center
background-size: cover

---
# The Data
<img src="categorical_predictors_files/figure-html/lizard_load-1.png" style="display: block; margin: auto;" />

---
# Looking at Means and SE
<img src="categorical_predictors_files/figure-html/lizard_mean-1.png" style="display: block; margin: auto;" />

---
# What is Really Going On?
<img src="categorical_predictors_files/figure-html/lizard_mean-1.png" style="display: block; margin: auto;" />
--
What if we think of Dead = 0, Living = 1

---
# Let's look at it a different way

.center[
![](images/all_linear_models/graph-me.png)
]

---
# First, Recode the Data with Dummy Variables
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> Squamosal horn length </th>
   <th style="text-align:right;"> Survive </th>
   <th style="text-align:left;"> Status </th>
   <th style="text-align:right;"> StatusDead </th>
   <th style="text-align:right;"> StatusLiving </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 13.1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.2 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.5 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 17.2 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 17.7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
</tbody>
</table>

---
# But with an Intercept, we don't need Two Dummy Variables
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> Squamosal horn length </th>
   <th style="text-align:right;"> Survive </th>
   <th style="text-align:left;"> Status </th>
   <th style="text-align:right;"> (Intercept) </th>
   <th style="text-align:right;"> StatusLiving </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 13.1 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.2 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.5 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 15.7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 17.2 </td>
   <td style="text-align:right;"> 0 </td>
   <td style="text-align:left;"> Dead </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 17.7 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:left;"> Living </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 1 </td>
  </tr>
</tbody>
</table>

.center[This is known as a Treatment Contrast structure]

---
# This is Just a Linear Regression
<img src="categorical_predictors_files/figure-html/unnamed-chunk-4-1.png" style="display: block; margin: auto;" />

`$$Length_i = \beta_0 + \beta_1 Status_i + \epsilon_i$$`

---

# You're Not a Dummy, Even If You Code a Dummy Variable

`$$Length_i = \beta_0 + \beta_1 Status_i + \epsilon_i$$`

- Setting `$Status_i$` to 0 or 1 (Dead or Living) is called Dummy Coding
     - Or One Hot Encoding in the ML world.

- We can always turn groups into "Dummy" 0 or 1

- We could even fit a model wit no `$\beta_0$` and code Dead = 0 or 1 and Living = 0 or 1

- This approach works for any **unordered categorical (nominal) variable**

---
class: center, middle

## The Only New Assumption-Related Thing is a More Gimlet Eye on Homogeneity of Variance

---
# Homogeneity of Variance Important for CI Estimation

---
# Dummy Codding for Dummy Models

1. The Categorical as Continuous.

2. .red[Many Levels of One Category]

3. Interpretation of Categorical Results.

4. Querying Your Model to Compare Groups

---
# Categorical Predictors: Gene Expression and Mental Disorders

.pull-left[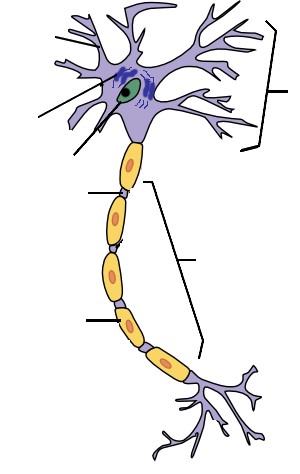
![](./images/19/neuron_label.jpeg)
]

.pull-right[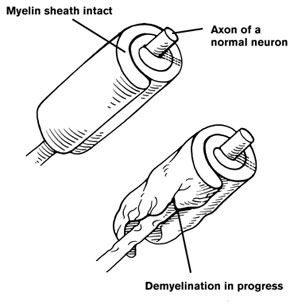
![](./images/19/myelin.jpeg)
]

---
# The data
<img src="categorical_predictors_files/figure-html/boxplot-1.png" style="display: block; margin: auto;" />

---
# Traditional Way to Think About Categories
<img src="categorical_predictors_files/figure-html/meansplot-1.png" style="display: block; margin: auto;" />

What is the variance between groups v. within groups?

---
# If We Only Had Control v. Bipolar...

---
# If We Only Had Control v. Bipolar...

Underlying linear model with control = intercept, dummy variable for bipolar

---

# If We Only Had Control v. Bipolar...

Underlying linear model with control = intercept, dummy variable for bipolar

---
# If We Only Had Control v. Schizo...

Underlying linear model with control = intercept, dummy variable for schizo

---

# If We Only Had Control v. Schizo...
<img src="categorical_predictors_files/figure-html/ctl_schizo-1.png" style="display: block; margin: auto;" />

Underlying linear model with control = intercept, dummy variable for schizo

---
# Linear Dummy Variable (Fixed Effect) Model
`$$\large y_{ij} = \beta_{0} + \sum \beta_{j}x_{ij} + \epsilon_{ij}, \qquad x_{i} = 0,1$$`  
`$$\epsilon_{ij} \sim N(0, \sigma^{2})$$`

- i = replicate, j = group

- `$x_{ij}$` inidicates presence/abscence (1/0) of level j for individual i  
     - A **Dummy variable**

- This is the multiple predictor extension of a two-category model

- All categories are *orthogonal*

- One category set to `$\beta_{0}$` for ease of fitting, and other `$\beta$`s are different from it

---
# A Simpler Way to Write: The Means Model
`$$\large y_{ij} = \alpha_{j} + \epsilon_{ij}$$`  
`$$\epsilon_{ij} \sim N(0, \sigma^{2} )$$`

- i = replicate, j = group

- Different mean for each group

- Focus is on specificity of a categorical predictor

---
# Partioning Model to See What Varies

`$$\large y_{ij} = \bar{y} + (\bar{y}_{j} - \bar{y}) + ({y}_{ij} - \bar{y}_{j})$$`

- i = replicate, j = group

- Shows partitioning of variation  
     - Between group v. within group variation

- Consider `$\bar{y}$` an intercept, deviations from intercept by treatment, and residuals

- Can Calculate this with a fit model to answer questions - it's a relic of a bygone era
     - That bygone era has some good papers, so, you should recognize this
     
     
---
# Let's Fit that Model

**Using Least Squares**

```r
brain_lm <- lm(PLP1.expression ~ group, data=brainGene)

tidy(brain_lm) |> 
  select(-c(4:5)) |>
  knitr::kable(digits = 3) |>
  kableExtra::kable_styling()
```

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> -0.004 </td>
   <td style="text-align:right;"> 0.048 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> groupschizo </td>
   <td style="text-align:right;"> -0.191 </td>
   <td style="text-align:right;"> 0.068 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> groupbipolar </td>
   <td style="text-align:right;"> -0.259 </td>
   <td style="text-align:right;"> 0.068 </td>
  </tr>
</tbody>
</table>

---

# Dummy Codding for Dummy Models

1. The Categorical as Continuous

2. Many Levels of One Category

3. .red[Interpretation of Categorical Results]

4. Querying Your Model to Compare Groups

---
# R Fits with Treatment Contrasts
`$$y_{ij} = \beta_{0} + \sum \beta_{j}x_{ij} + \epsilon_{ij}$$`

What does this mean?

- Intercept ($\beta_{0}$) = the average value associated with being in the control group

- Others = the average difference between control and each other group

- Note: Order is alphabetical

---
# Actual Group Means

`$$y_{ij} = \alpha_{j} + \epsilon_{ij}$$`

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> group </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> control </td>
   <td style="text-align:right;"> -0.0040000 </td>
   <td style="text-align:right;"> 0.0479786 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> schizo </td>
   <td style="text-align:right;"> -0.1953333 </td>
   <td style="text-align:right;"> 0.0479786 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> bipolar </td>
   <td style="text-align:right;"> -0.2626667 </td>
   <td style="text-align:right;"> 0.0479786 </td>
  </tr>
</tbody>
</table>

What does this mean?

Being in group j is associated with an average outcome of y.

---

# What's the best way to see this?
.center[ ![:scale 75%](./images/anova/barplot_viz.jpg)]

---
# Many Ways to Visualize

---
# Many Ways to Visualize

---
# Many Ways to Visualize

---
# How Well Do Groups Explain Variation in Response Data?

We can look at fit to data - even in categorical data!

```
# R2 for Linear Regression
       R2: 0.271
  adj. R2: 0.237
```

But, remember, this is based on the sample at hand.

Adjusted R<sup>2</sup>: adjusts for sample size and model complexity (k = # params = # groups)

`$$R^2_{adj} = 1 - \frac{(1-R^2)(n-1)}{n-k-1}$$`

---

# Dummy Codding for Dummy Models

1. The Categorical as Continuous

2. Many Levels of One Category

3. Interpretation of Categorical Results.

4. .red[Querying Your Model to Compare Groups]

---
# Which groups are different from each other?
<img src="categorical_predictors_files/figure-html/meansplot-1.png" style="display: block; margin: auto;" />

Many mini-linear models with two means....multiple comparisons!

---
# Post-Hoc Means Comparisons: Which groups are different from one another?

- Each group has a mean and SE

- We can calculate a comparison for each

- BUT, we lose precision as we keep resampling the model  
  
- Remember, for every time we look at a system, we have some % of our CI not overlapping the true value

- Each time we compare means, we have a chance of our CI not covering the true value

- To minimize this possibility, we correct (widen) our CIs for this **Family-Wise Error Rate**

---
# Solutions to Multiple Comparisons and Family-wise Error Rate?

1. Ignore it - 
     + Just a bunch of independent linear models

--
2. Increase your CI given m = # of comparisons
     + If 1 - CI of interest = `$\alpha$`  
     + Bonferroni Correction `$\alpha/ = \alpha/m$`
     + False Discovery Rate `$\alpha/ = k\alpha/m$` where k is rank of test

--
3. Other multiple comparison corrections
    + Tukey's Honestly Significant Difference  
    + Dunnett's Compare to Control

---

# No Correction: Least Square Differences
<table class="table table-striped" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> contrast </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> control - schizo </td>
   <td style="text-align:right;"> 0.1913333 </td>
   <td style="text-align:right;"> 0.0544024 </td>
   <td style="text-align:right;"> 0.3282642 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> control - bipolar </td>
   <td style="text-align:right;"> 0.2586667 </td>
   <td style="text-align:right;"> 0.1217358 </td>
   <td style="text-align:right;"> 0.3955976 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> schizo - bipolar </td>
   <td style="text-align:right;"> 0.0673333 </td>
   <td style="text-align:right;"> -0.0695976 </td>
   <td style="text-align:right;"> 0.2042642 </td>
  </tr>
</tbody>
</table>

---
# Bonferroni Corrections
<table class="table table-striped" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> contrast </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> control - schizo </td>
   <td style="text-align:right;"> 0.1913333 </td>
   <td style="text-align:right;"> 0.0221330 </td>
   <td style="text-align:right;"> 0.3605337 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> control - bipolar </td>
   <td style="text-align:right;"> 0.2586667 </td>
   <td style="text-align:right;"> 0.0894663 </td>
   <td style="text-align:right;"> 0.4278670 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> schizo - bipolar </td>
   <td style="text-align:right;"> 0.0673333 </td>
   <td style="text-align:right;"> -0.1018670 </td>
   <td style="text-align:right;"> 0.2365337 </td>
  </tr>
</tbody>
</table>

---
# Tukey's Honestly Significant Difference
<table class="table table-striped" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> contrast </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> control - schizo </td>
   <td style="text-align:right;"> 0.1913333 </td>
   <td style="text-align:right;"> 0.0264873 </td>
   <td style="text-align:right;"> 0.3561793 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> control - bipolar </td>
   <td style="text-align:right;"> 0.2586667 </td>
   <td style="text-align:right;"> 0.0938207 </td>
   <td style="text-align:right;"> 0.4235127 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> schizo - bipolar </td>
   <td style="text-align:right;"> 0.0673333 </td>
   <td style="text-align:right;"> -0.0975127 </td>
   <td style="text-align:right;"> 0.2321793 </td>
  </tr>
</tbody>
</table>

---
# Visualizing Comparisons (Tukey)
<img src="categorical_predictors_files/figure-html/tukey-viz-1.png" style="display: block; margin: auto;" />

---
# Dunnett's Comparison to Controls
<table class="table table-striped" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> contrast </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> conf.low </th>
   <th style="text-align:right;"> conf.high </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> schizo - control </td>
   <td style="text-align:right;"> -0.1913333 </td>
   <td style="text-align:right;"> -0.3474491 </td>
   <td style="text-align:right;"> -0.0352176 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> bipolar - control </td>
   <td style="text-align:right;"> -0.2586667 </td>
   <td style="text-align:right;"> -0.4147824 </td>
   <td style="text-align:right;"> -0.1025509 </td>
  </tr>
</tbody>
</table>

---

# So, Categorical Models...

- At the end of the day, they are just another linear model  
  
- We can understand a lot about groups, though

- We can begin to see the value of queries/counterfactuals

`$$\widehat {\textbf{Y} } = \textbf{X}\beta$$`
`$$\textbf{Y} \sim \mathcal{N}(\widehat {\textbf{Y} }, \Sigma)$$`