It’s All Linear Models

class: center, middle

# It's All Linear Models: T-Test Edition

![image](./images/all_linear_models/linear_regression_everywhere.jpg)

---
class: center, middle

# Etherpad
<br><br>
<center><h3>https://etherpad.wikimedia.org/p/607-linear_everywhere-2020</h3></center>

---
# YES, YOU KNOW EVERYTHING

1. Beastiary of Everything As a Linear Model

2. T-Tests as a Linear Model

---
# Up until now, we've done this
`$$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$$`
`$$\epsilon_i \sim N(0, \sigma)$$`

---

# But we have wider classes of problems...
### Comparing Two Means

--
`$$mass_i = \beta_0 + \beta_1 sex_i + \epsilon_i$$`
---

# But we have wider classes of problems...
### Comparing Many Means

--
`$$mass_i =  \beta_1 adelie_i + \beta_2 chinstrap_i + \beta_3 gentoo_i + \epsilon_i$$`
---

# But we have wider classes of problems...
### Many Predictors

<img src="t_as_lm_files/figure-html/unnamed-chunk-3-1.png" style="display: block; margin: auto;" />
--
$$length_i = \beta_0 + \beta_1 flipper_i + \beta_2 depth_i+ \epsilon_i  $$
---

# But we have wider classes of problems...
### One Predictor Modifies Another
<img src="t_as_lm_files/figure-html/unnamed-chunk-4-1.png" style="display: block; margin: auto;" />

--
`$$\small flipper_i = \beta_0 mass_i + \beta_1 adelie_i + \beta_2 chinstrap_i + \beta_3 gentoo_i +$$`
$$\small\beta_4 mass_iadelie_i + \beta_5 mass_ichinstrap_i + \beta_6 mass_igentoo_i + \epsilon_i  $$
---
class:center, middle
![:scale 65%](images/all_linear_models/glm_meme.png)
---

# But we have wider classes of problems...
### Nonlinear Models and Transformation

`$$log(bmr_i) = log(\beta_0) + \beta_1 log(mass_i) + \epsilon_i$$`
`$$bmr_i = \beta_0 mass_i^{\beta_1}  \epsilon_i$$`
---

# But we have wider classes of problems...
### Non-Normal Nonlinear Models
<img src="t_as_lm_files/figure-html/crypto_data-1.png" style="display: block; margin: auto;" />

`$$infected_i \sim B(prob.\ infected_i, size = trials)$$`
`$$logit(prob.\ infected_i) = \beta_0 + \beta_1 Dose_i$$`
---

# But we have wider classes of problems...
### Goodness of Fit
.pull-left[
<table class="table table-striped" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> Day of the Week </th>
   <th style="text-align:right;"> Births </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> Sunday </td>
   <td style="text-align:right;"> 33 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Monday </td>
   <td style="text-align:right;"> 41 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Tuesday </td>
   <td style="text-align:right;"> 63 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Wednesday </td>
   <td style="text-align:right;"> 63 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Thursday </td>
   <td style="text-align:right;"> 47 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Friday </td>
   <td style="text-align:right;"> 56 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Saturday </td>
   <td style="text-align:right;"> 47 </td>
  </tr>
</tbody>
</table>
]

.pull-right[
<img src="t_as_lm_files/figure-html/unnamed-chunk-6-1.png" style="display: block; margin: auto;" />
]
--

`$$births_i \sim P(\widehat{births_i})$$`
`$$log(\widehat{births_i}) = \beta_1Monday_i + \beta_2Tuesday_i+...$$`

---

# But we have wider classes of problems...
### Contingency Tables

.pull-left[
![](./images/10/eizaguirre_lab_fish_parasite.jpg)

]

.pull-right[
<img src="t_as_lm_files/figure-html/unnamed-chunk-7-1.png" style="display: block; margin: auto;" />
]

`$$count_i \sim P(\widehat{count_i})$$`
`$$log(\widehat{count_i}) = \beta_1eaten_i + \beta_2infection_i+ \beta_3 eaten_i *infection_i$$`

---
# IT'S ALL VARIANTS OF A (GENERALIZED) LINEAR MODEL

`$$\large f(\widehat{y_i}) = \beta_0 + \beta_1 x1_i + \beta_2 x2_i + \ldots$$`

<br>
  
`$$\large y_i \sim Dist(mean = \widehat{y_i}, dispersion = s(\widehat{y_i}))$$`

- X can be continuous OR discrete (turned into 1 and 0)   
- Y can be continous, ranks, etc.  
- f(Y) can be an identity, log, logit, or other relationship  
- Dist can be normal, or really anything  
- s(Y) can be just a single number, a linear, or nonlinear function

---
class:center, middle

![](images/all_linear_models/Gump-Linear-Regression-company.jpg)

---
# YES, YOU KNOW EVERYTHING

1. Beastiary of Everything As a Linear Model

2. .red[T-Tests as a Linear Model]

---
# Classical Approach: T-test
![](images/09/t_distribution.png)

---
# Classical Approach: T-test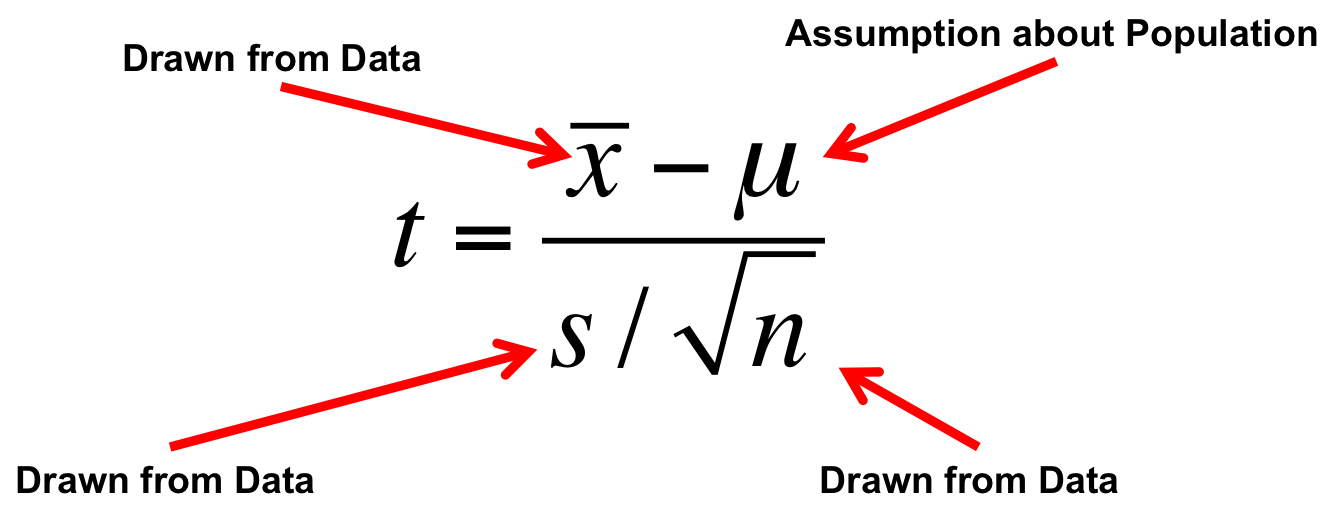
![](images/09/t.png)

---

# The One-Sample T-Test

- We take some data

- We estimate it's mean and SE

- We calculate whether it is different from some hypothesis (usually 0)

- But.... isn't this just an intercept only model?

`$$\Large y_i = \beta_0 + \epsilon_i$$`

---

# Consider Climate-Change Driven Range Shifts

- Is the distribution of range-shifts 0?

.small[Chen, I-C., J. K. Hill, R. Ohlemüller, D. B. Roy, and C,. D. Thomas. 2011. Science 333:1024-1026.]

---

# Testing a Mean with an Intercept Only Model

```r
shift_mod <- lm(elevationalRangeShift ~ 1, data = shift)

shift_t <- t.test(shift$elevationalRangeShift)
```

LM Coefficients versus T-Test
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> 39.32903 </td>
   <td style="text-align:right;"> 5.507258 </td>
   <td style="text-align:right;"> 7.141309 </td>
   <td style="text-align:right;"> 1e-07 </td>
  </tr>
</tbody>
</table>

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 39.32903 </td>
   <td style="text-align:right;"> 7.141309 </td>
   <td style="text-align:right;"> 1e-07 </td>
  </tr>
</tbody>
</table>

---

# What if we are looking at Change Between Pairs

- Classically, we have the **Paired T-Test**

- We look at differences between pairs
     - Could be One Individual over time
     - Could be two plots next to each other
     - Deliciously simple
     
- This is just an intercept only model where the Difference is our response variable

`$$\Large (y1 - y2)_i = \beta_0 + \epsilon_i$$`
---
# Does bird immunococompetence decrease after a testosterone implant?
.center[
![](images/09/blackbird.jpg)
]

---
# Differences in Antibody Performance
<img src="t_as_lm_files/figure-html/blackbird_plot-1.png" style="display: block; margin: auto;" />

---
# Again, Intercept Only Model v. T-Test

LM Coefficients versus T-Test
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> (Intercept) </td>
   <td style="text-align:right;"> 6.538462 </td>
   <td style="text-align:right;"> 4.336215 </td>
   <td style="text-align:right;"> 1.507873 </td>
   <td style="text-align:right;"> 0.157455 </td>
  </tr>
</tbody>
</table>

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 6.538462 </td>
   <td style="text-align:right;"> 1.507873 </td>
   <td style="text-align:right;"> 0.157455 </td>
  </tr>
</tbody>
</table>

---
# Consider Comparing Two Means
#### Consider the Horned Lizard 
.center[
![:scale 50%](images/09/horned_lizard.jpg)
]

Horns prevent these lizards from being eaten by birds. Are horn lengths different between living and dead lizards, indicating selection pressure?

---
# The Data
<img src="t_as_lm_files/figure-html/lizard_load-1.png" style="display: block; margin: auto;" />

---
# Looking at Means and SE
<img src="t_as_lm_files/figure-html/lizard_mean-1.png" style="display: block; margin: auto;" />

---
# What is Really Going On?
<img src="t_as_lm_files/figure-html/lizard_mean-1.png" style="display: block; margin: auto;" />
--
What if we think of Dead = 0, Living = 1

---
# Let's look at it a different way

.center[
![](images/all_linear_models/graph-me.png)
]
---
# This is Just a Linear Regression
<img src="t_as_lm_files/figure-html/unnamed-chunk-11-1.png" style="display: block; margin: auto;" />

`$$Length_i = \beta_0 + \beta_1 Status_i + \epsilon_i$$`
---
# You're Not a Dummy, Even if Your Code Is

`$$Length_i = \beta_0 + \beta_1 Status_i + \epsilon_i$$`

- Setting `$Status_i$` to 0 or 1 (Dead or Living) is called Dummy Coding

- We can always turn groups into "Dummy" 0 or 1

- We could even fit a model wit no `$\beta_0$` and code Dead = 0 or 1 and Living = 0 or 1

- This approach works for any **nominal variable**

---
# How Do We Analyze This?

- T-Test of Coefficients tells you difference between dead and live

- Wait, did you say **T-Test**?
     - Yes, we're doing *the same thing* in coefficient evaluation
     
--

- F-tests still useful for looking at variation explained
    - Also `$R^2$`
    
--

- You can even use likelihood, Bayes, CV, and other tools

- You get more for your money with linear models!

---
# Fit and Compare!

```r
t_mod <- lm(`Squamosal horn length` ~ Status, 
            data = lizards)
```

Coefficients from Linear Model:
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> StatusLiving </td>
   <td style="text-align:right;"> 2.294502 </td>
   <td style="text-align:right;"> 0.5275497 </td>
   <td style="text-align:right;"> 4.349358 </td>
   <td style="text-align:right;"> 2.27e-05 </td>
  </tr>
</tbody>
</table>

T-Test
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> estimate1 </th>
   <th style="text-align:right;"> estimate2 </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> -2.294502 </td>
   <td style="text-align:right;"> 21.98667 </td>
   <td style="text-align:right;"> 24.28117 </td>
   <td style="text-align:right;"> -4.349358 </td>
   <td style="text-align:right;"> 2.27e-05 </td>
  </tr>
</tbody>
</table>

---
# Variatons on a theme: Non-Parametric Mann-Whitney U

How about those residuals?

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
   <th style="text-align:left;"> method </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 0.9602582 </td>
   <td style="text-align:right;"> 4.58e-05 </td>
   <td style="text-align:left;"> Shapiro-Wilk normality test </td>
  </tr>
</tbody>
</table>

Classical approach: Non-Parametric Mann-Whitney-U Test

- But, are you really going to remember that?

- Simpler to remember, we just transform Y values to ranks, and voila, we have a general technique

---
# Signed Rank versus Original Values

---
# Signed Rank as Data

---
# Signed Rank as Boxplots

---
# Variations on a theme: Welch's T-Test

```r
mwu_mod <- lm(rank(`Squamosal horn length`) ~ Status, 
            data = lizards)

mwu <- wilcox.test(`Squamosal horn length` ~ Status, 
            data = lizards,)
```

Linear Model on Ranks
<table>
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> StatusLiving </td>
   <td style="text-align:right;"> 44.94459 </td>
   <td style="text-align:right;"> 10.12238 </td>
   <td style="text-align:right;"> 4.440119 </td>
   <td style="text-align:right;"> 1.56e-05 </td>
  </tr>
</tbody>
</table>

Mann-Whitney-U/Wilcoxon Rank Test
<table>
 <thead>
  <tr>
   <th style="text-align:right;"> MWU_p_value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 2.37e-05 </td>
  </tr>
</tbody>
</table>

---
# Variations on a theme: Welch's T-Test

Or.... let variance be different between groups.
i = data point, j = group

`$$y_{ij} = \beta_0 + \beta_1x_j + \epsilon_{ij}$$`
`$$\epsilon_{ij} \sim N(0, \sigma_j)$$`

Fit using **weighted least squares** - we weight LS by inverse of variance

Classically, this is known as Welch's T-Test, and is the default for R
   - Computes a pooled variance based on unequal variance/sample size

---
# Weighting by Variance

```r
library(nlme)
weighted_mod <- gls(squamosal_horn_length ~ Status,
                  weights = varIdent(form = ~1|Status),
                  data = lizards,
                  method = "ML")
```

Weighted Least Squares Results
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> term </th>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> std.error </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> StatusLiving </td>
   <td style="text-align:right;"> 2.294502 </td>
   <td style="text-align:right;"> 0.5331879 </td>
   <td style="text-align:right;"> 4.303365 </td>
   <td style="text-align:right;"> 2.74e-05 </td>
  </tr>
</tbody>
</table>

Welch's T-Test Results
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:right;"> estimate </th>
   <th style="text-align:right;"> estimate1 </th>
   <th style="text-align:right;"> estimate2 </th>
   <th style="text-align:right;"> statistic </th>
   <th style="text-align:right;"> p.value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> -2.294502 </td>
   <td style="text-align:right;"> 21.98667 </td>
   <td style="text-align:right;"> 24.28117 </td>
   <td style="text-align:right;"> -4.26337 </td>
   <td style="text-align:right;"> 0.0001178 </td>
  </tr>
</tbody>
</table>
---
# Don't forget...

.center[

![:scale 55%](images/all_linear_models/i-dont-always-5acc6f.jpg)

]
---
# Excess Baggage

- In this framework, you have to do ALL assumption tests

- BUT, t-tests have THE SAME ASSUMPTIONS

- BECASUE THEY ARE JUST LINEAR MODELS RE-ARRANGED

- AND, you gain flexibility in execution

- AND, you don't have to remember an arcane taxonomy of tests

`$$\large Y = \beta X + \epsilon$$`

---
# Care for Your Golem
.center[
![:scale 50%](images/09/golem.png)

Just remember, if you are not careful, even with the simplest data, you can still burn down Prague!]

---
class: center, middle

![:scale 55%](images/all_linear_models/curve-fitting-methods-and-the-messages-they-send-quadratic-logarithmic-linear-63265166.png)