Information Theoretic Approaches to Model Selection

What causes species richness?

• Distance from fire patch
• Elevation
• Abiotic index
• Patch age
• Patch heterogeneity
• Severity of last fire
• Plant cover

We could build a full model…

keeley_full <- lm(rich ~  elev + abiotic + hetero +
                          distance + firesev + 
                          age + cover,
                  data = keeley)

Consider this data…

sppnames <- c( "afarensis","africanus",
               "habilis","boisei",
               "rudolfensis","ergaster","sapiens")

brainvolcc <- c( 438 , 452 , 612, 521, 752, 871, 1350 )
masskg <- c( 37.0 , 35.5 , 34.5 , 41.5 , 55.5 , 61.0 , 53.5 )

d <- data.frame( species=sppnames, 
                 brain=brainvolcc, 
                 mass=masskg )

Underfitting

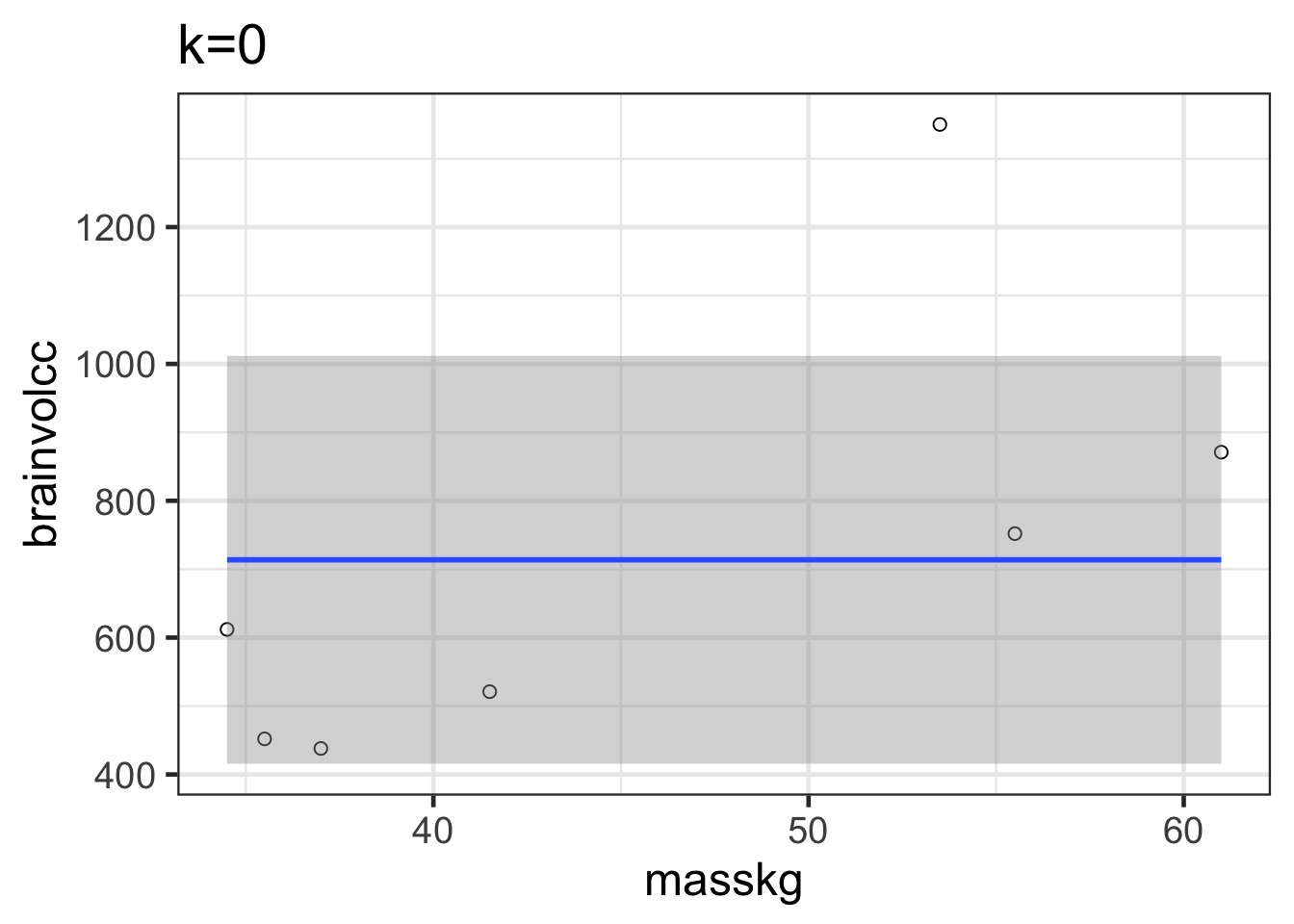
We have explained nothing!

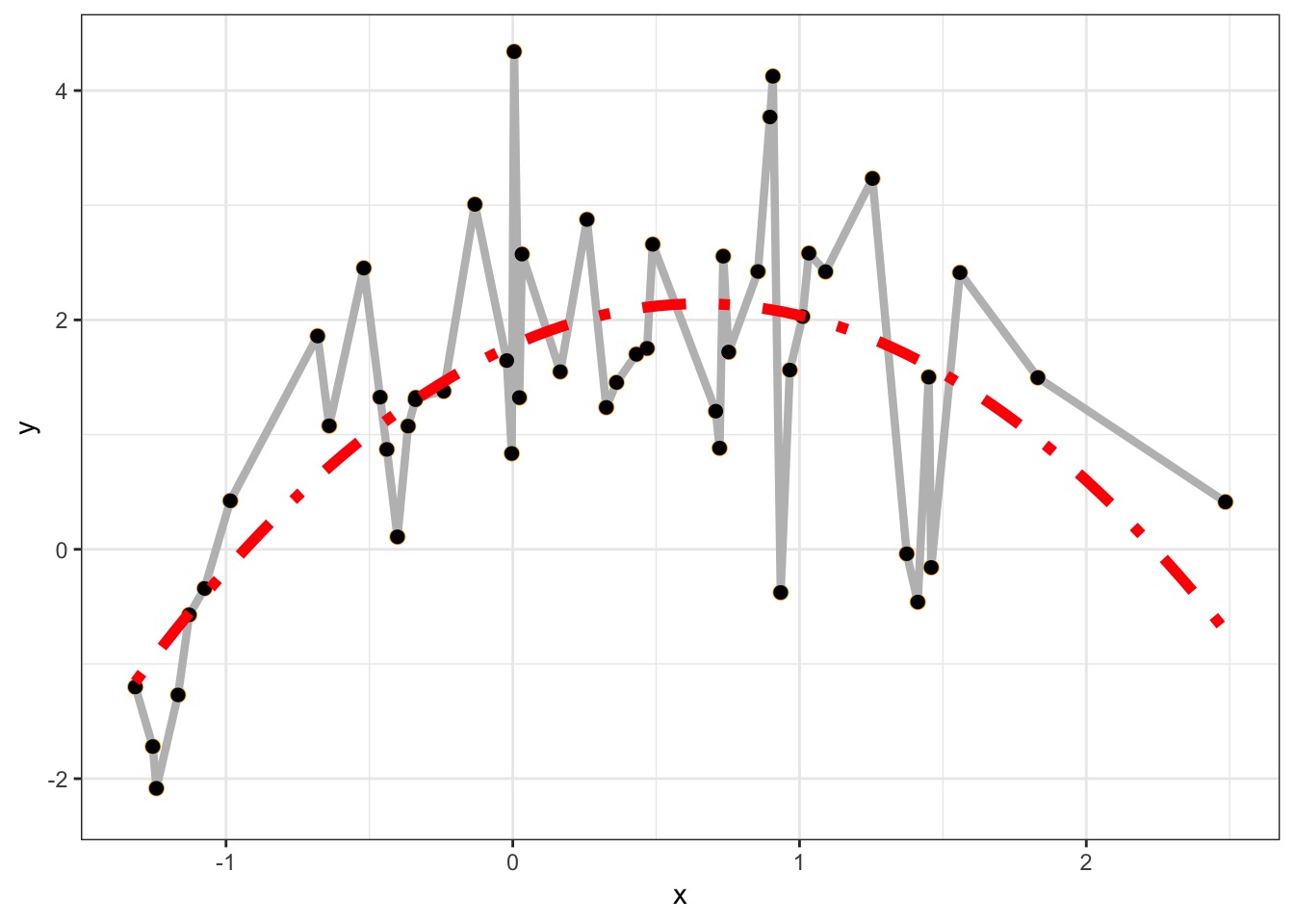
Overfitting

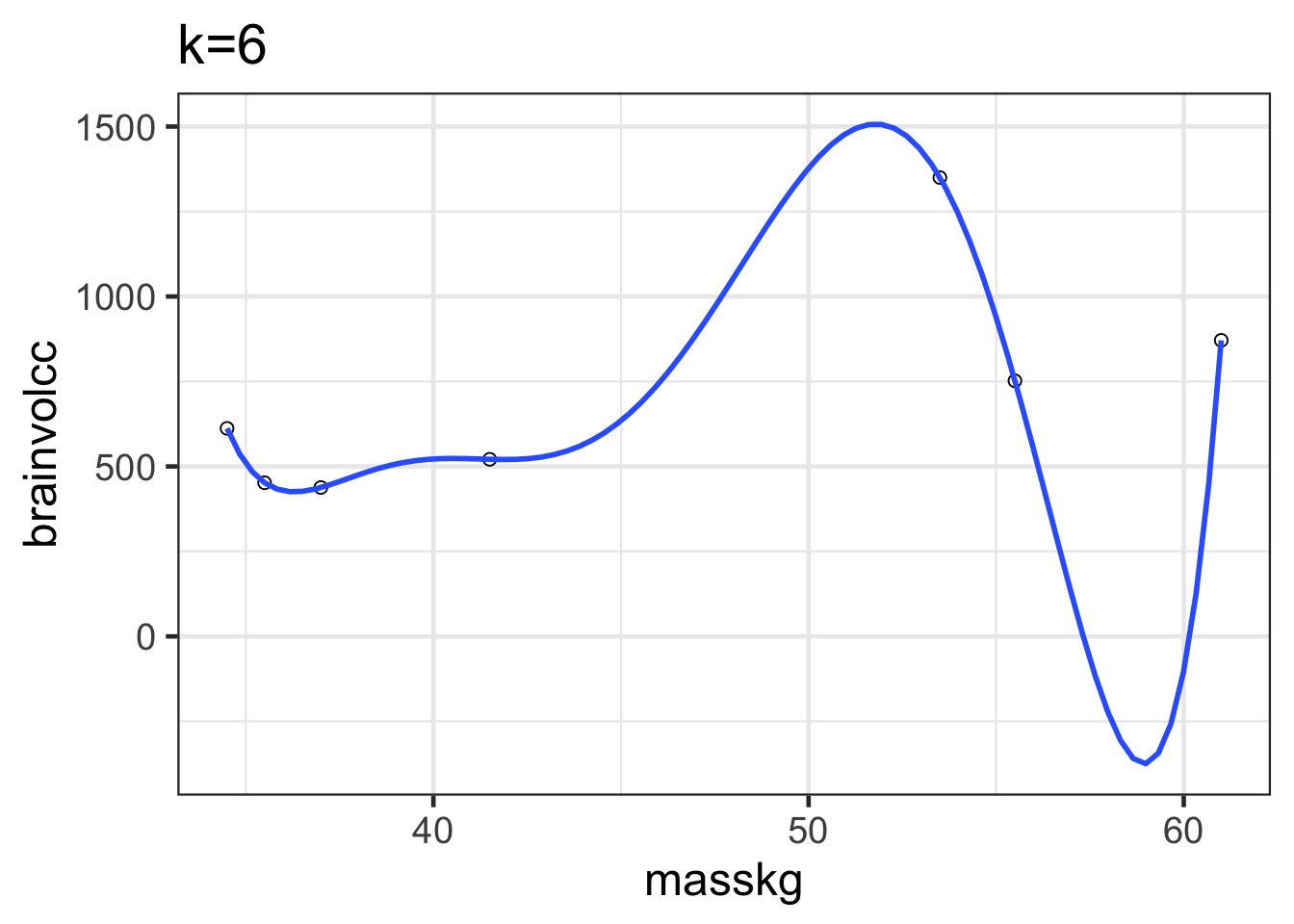
We have perfectly explained this sample

What is the right fit?

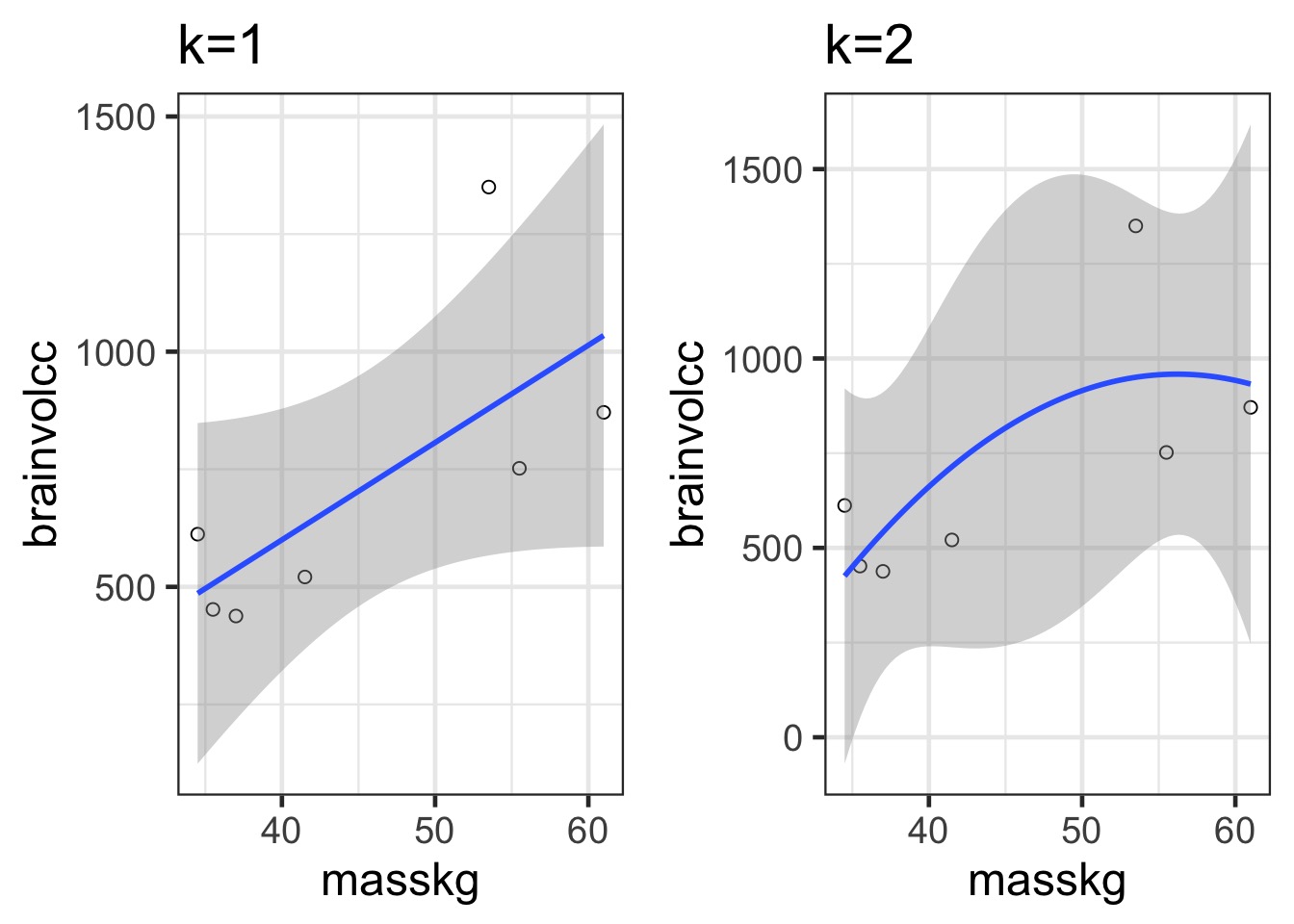
How complex a model do you need to be useful?

Some models are simple but good enough

More Complex Models are Not Always Better or Right

How do we Navigate Between Scylla and Charybdis?

1. Regularization
   • Penalize parameters with weak support
     
     
2. Optimization for Prediction
   • Information Theory
     
   • Draws from comparison of information loss

Model Selection in a Nutshell

• The Frequentist P-Value testing framework emphasizes the evaluation of a single hypothesis - the null. We evaluate whether we reject the null.
  
  
• This is perfect for an experiment where we are evaluating clean causal links, or testing for a a predicted relationship in data.
  
  
• Often, though, we have multiple non-nested hypotheses, and wish to evaluate each. To do so we need a framework to compare the relative amount of information contained in each model and select the best model or models. We can then evaluate the individual parameters.

In and Out of Sample Deviance

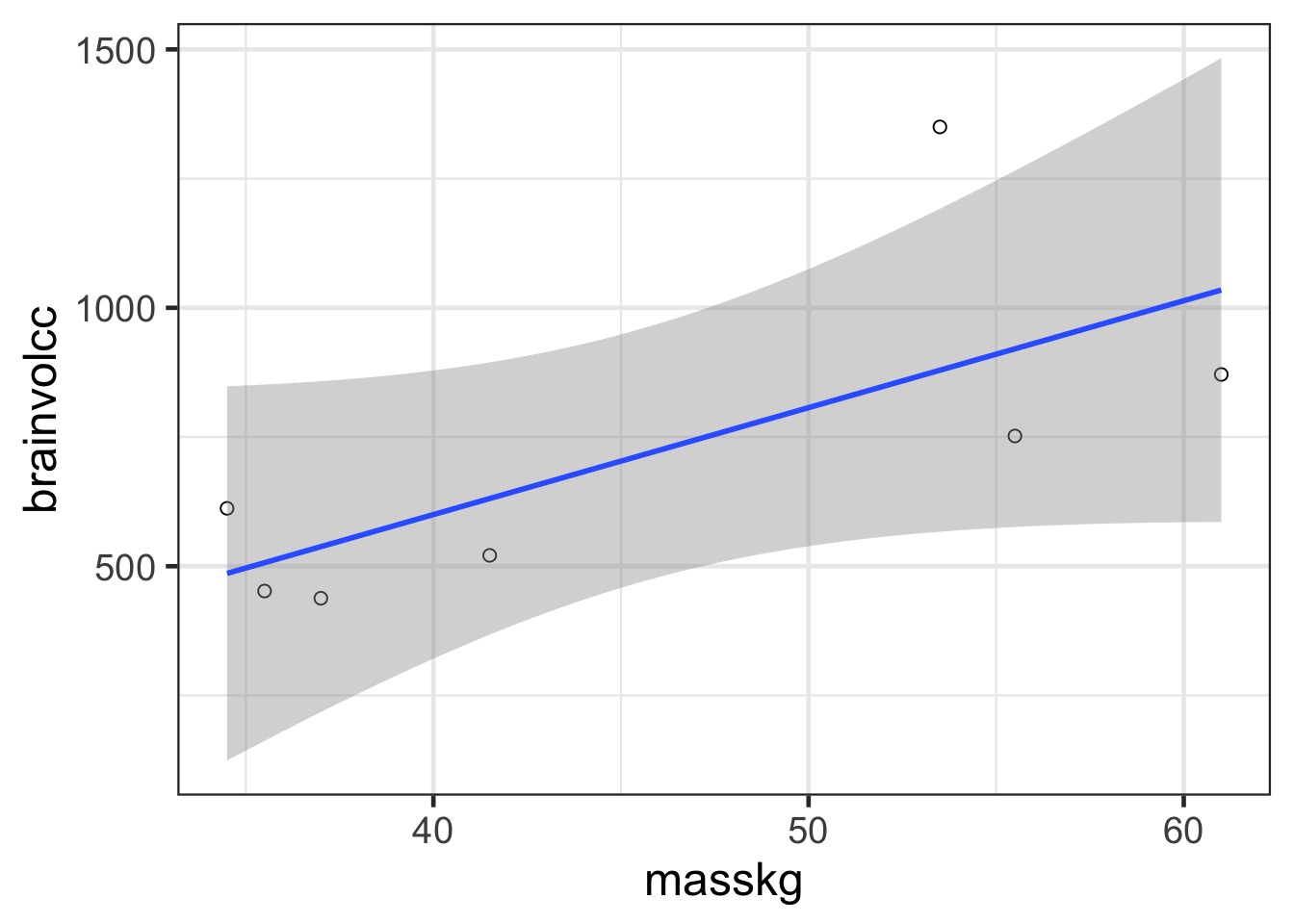
In and Out of Sample Deviance

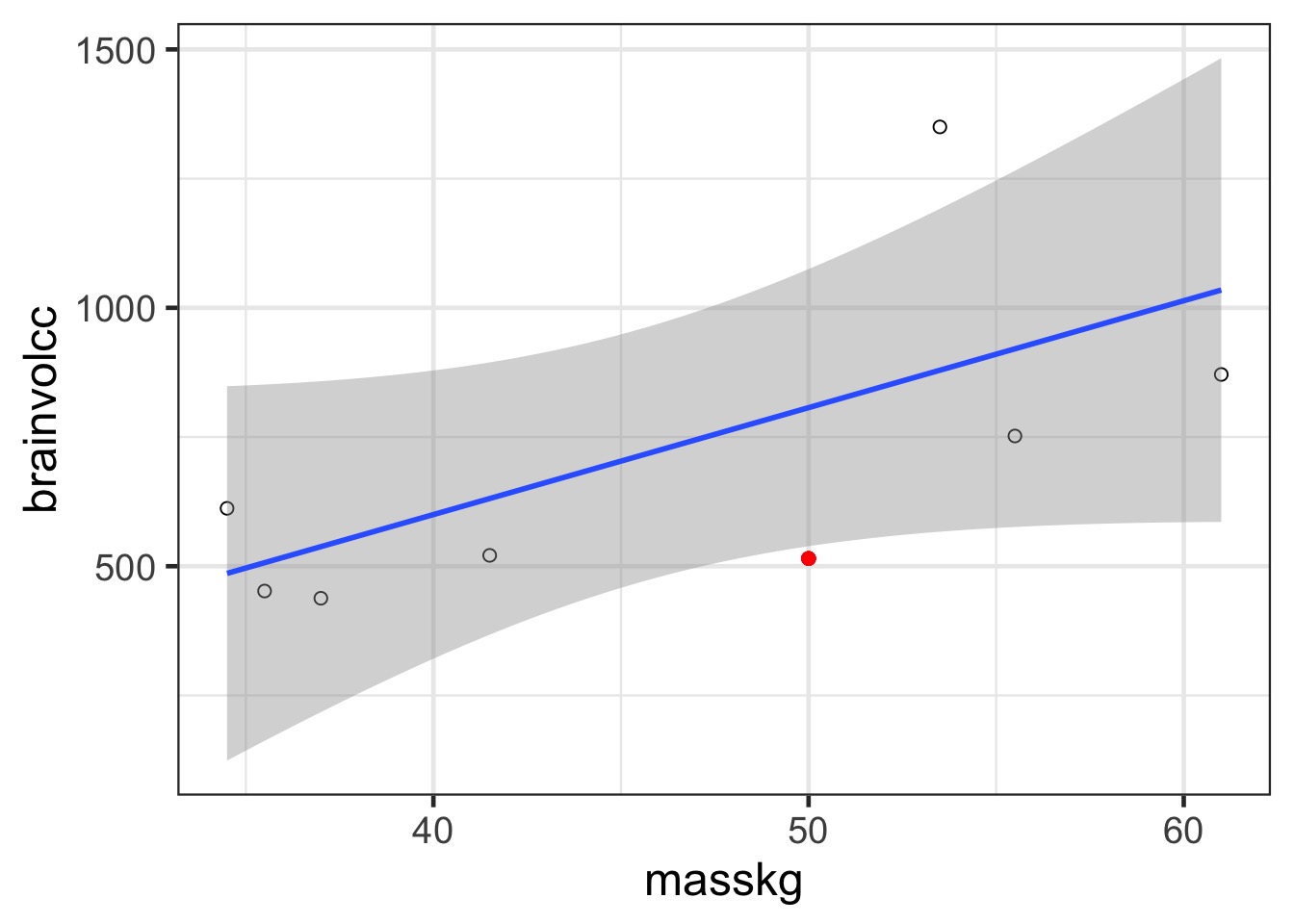
Prediction: 806.8141456, Observe: 515
Deviance: 8.526583810^{4}

Prediction: A Goal for Judging Models

• Can we minimize the out of sample deviance?
  
  
• So, fit a model, and evaluate how different the deviance is for a training versus test data set is
  
  
• This is called CROSS-VALIDATION

In and Out of Sample Deviance

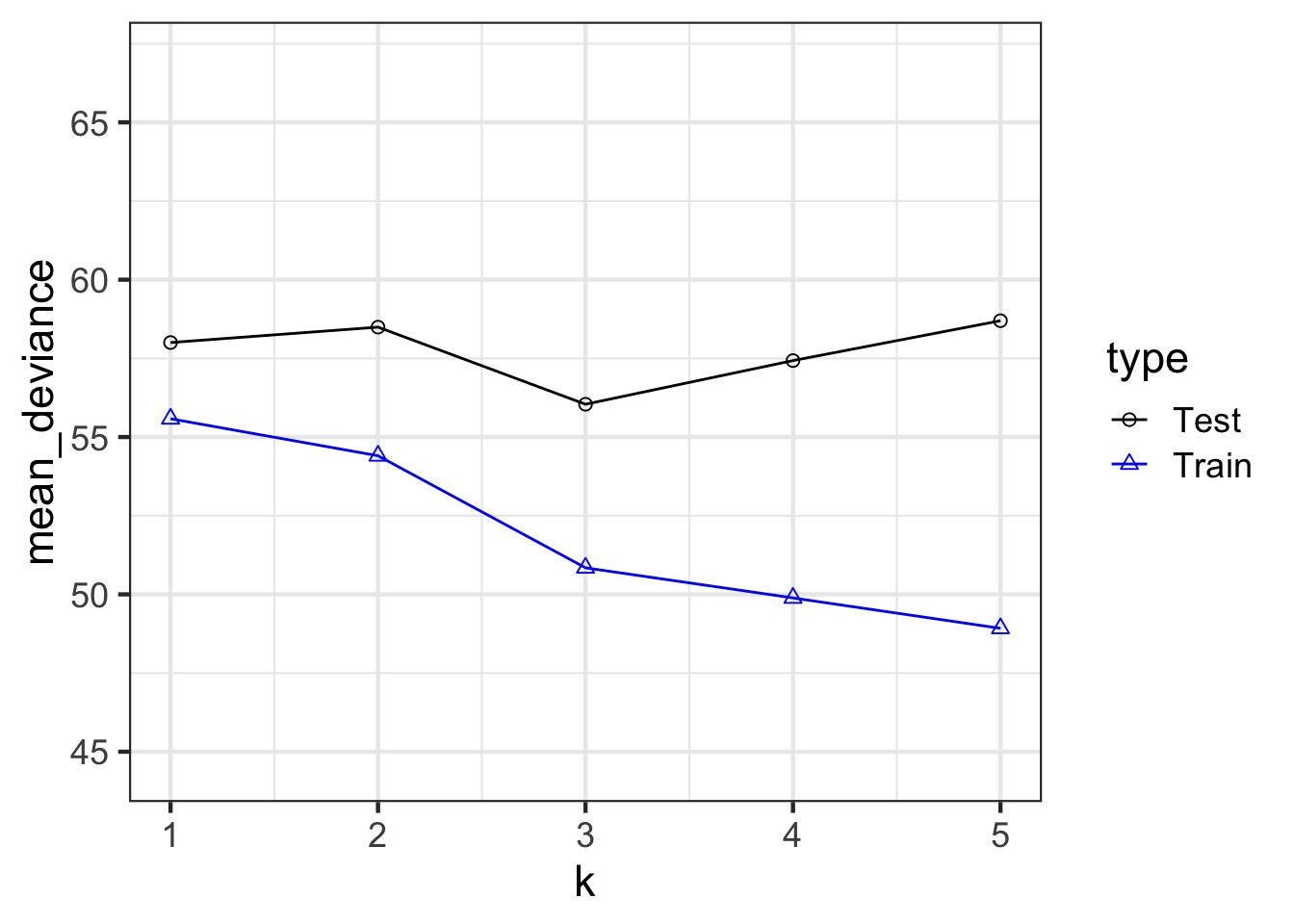
A Criteria Estimating Test Sample Deviance

• We don’t always have enough data for a “test” dataset
  
  
• What if we could estimate out of sample deviance?
  
  
• The difference between training and testing deviance shows overfitting
  
  

What’s the difference between train and test deviance?

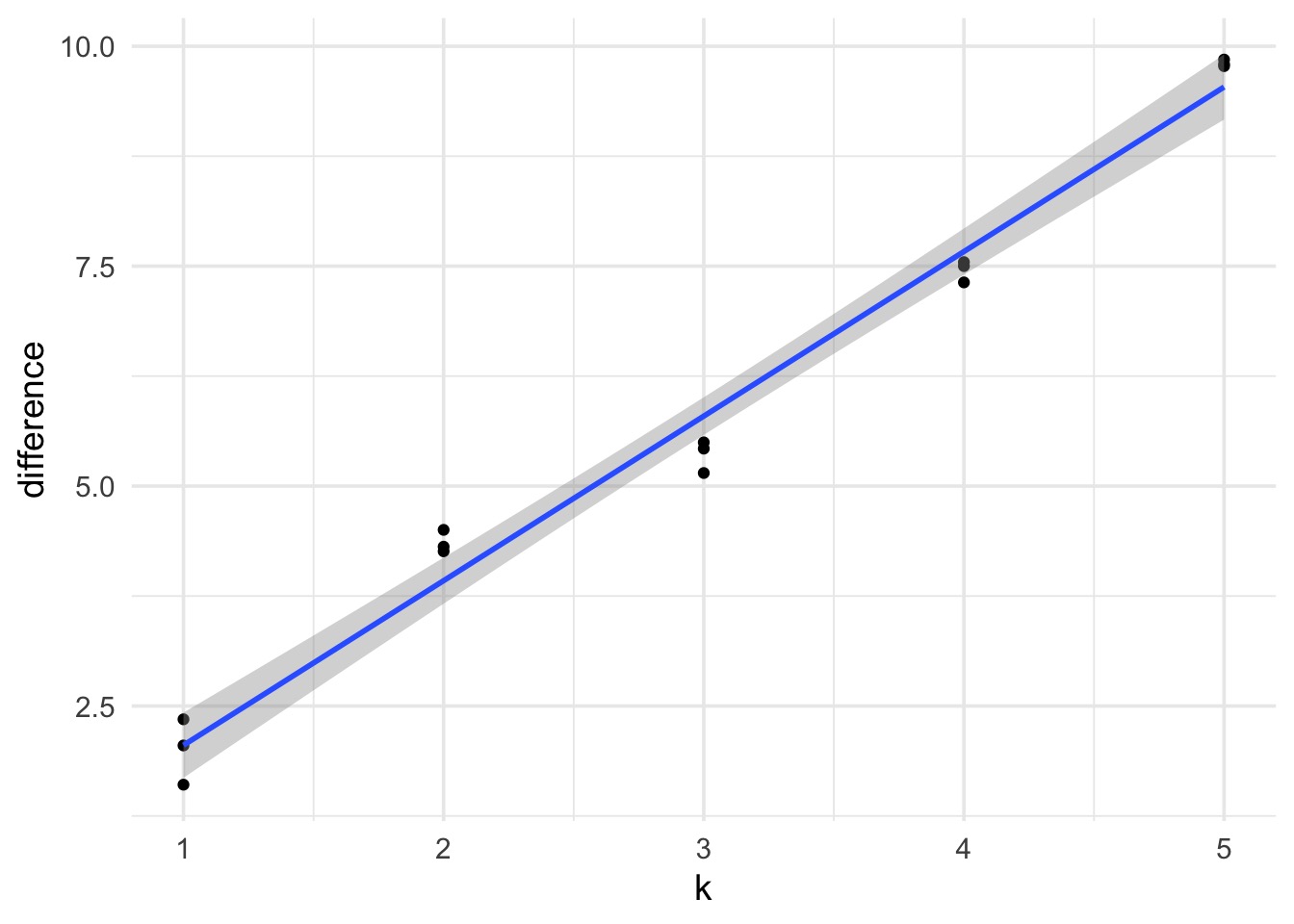
Slope of 1.87 (~2)

Enter the AIC

\[AIC = Deviance + 2K\]

Suppose this is the Truth

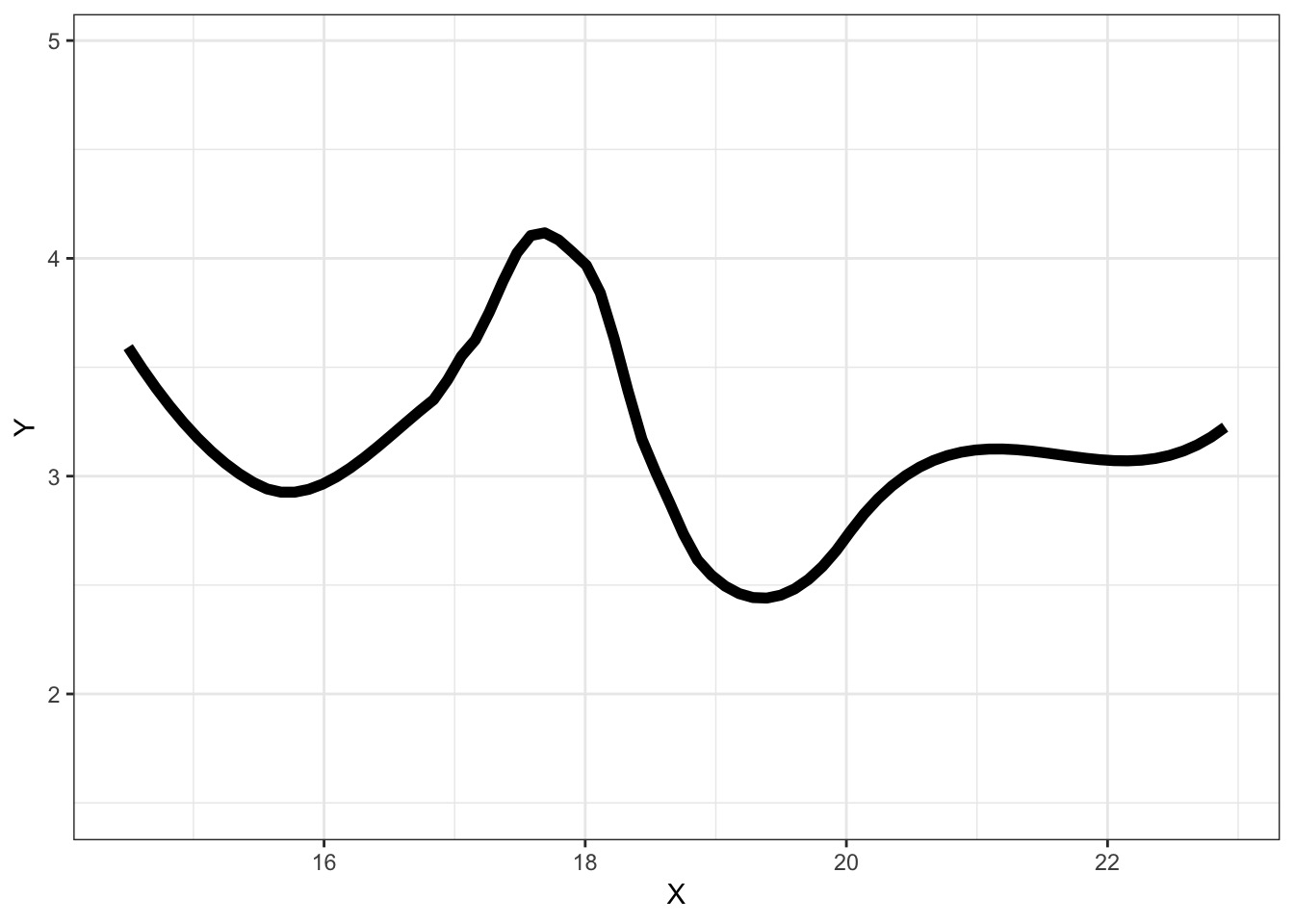
We Can Fit a Model To Descibe Our Data, but it Has Less Information

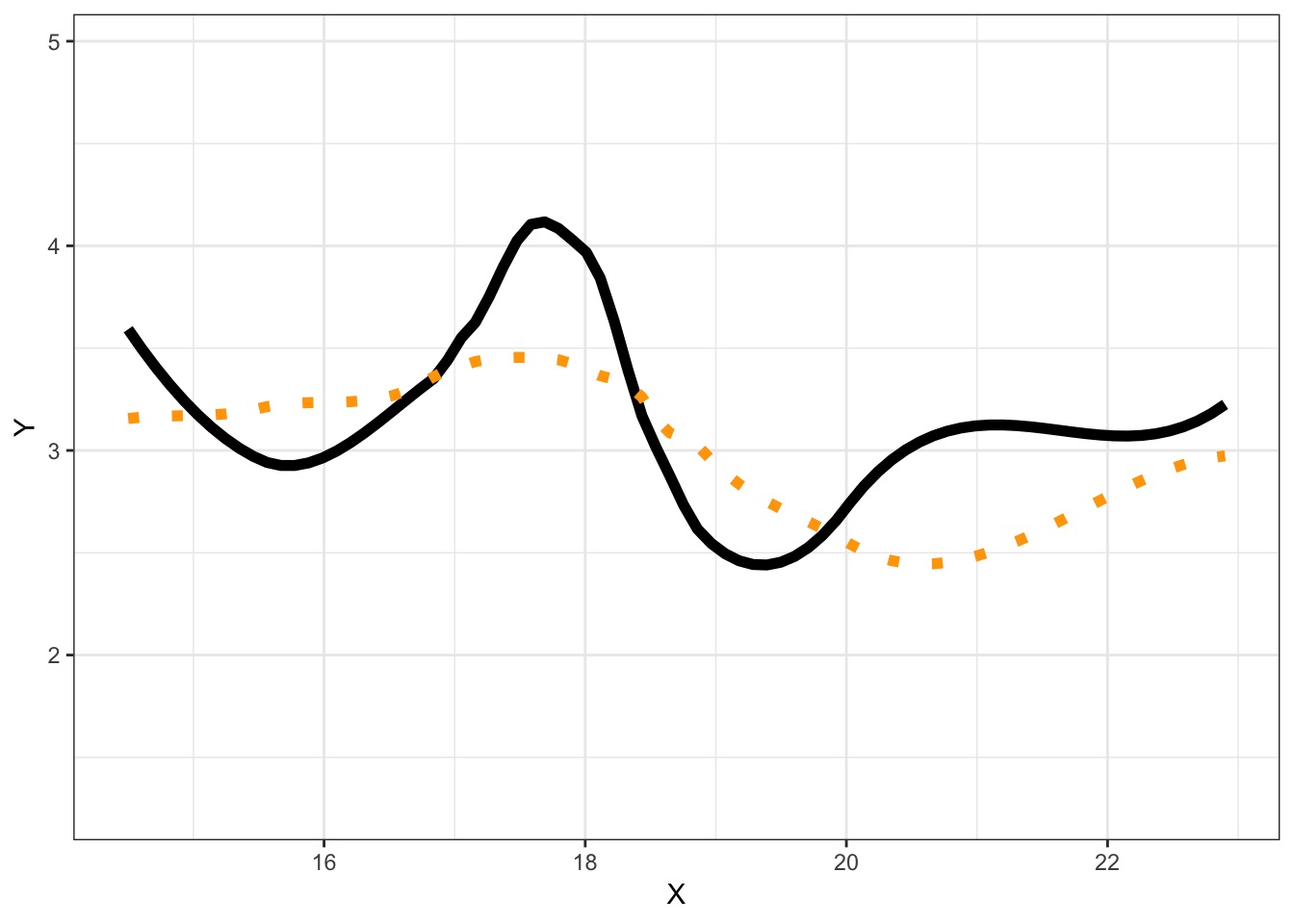
We Can Fit a Model To Descibe Our Data, but it Has Less Information

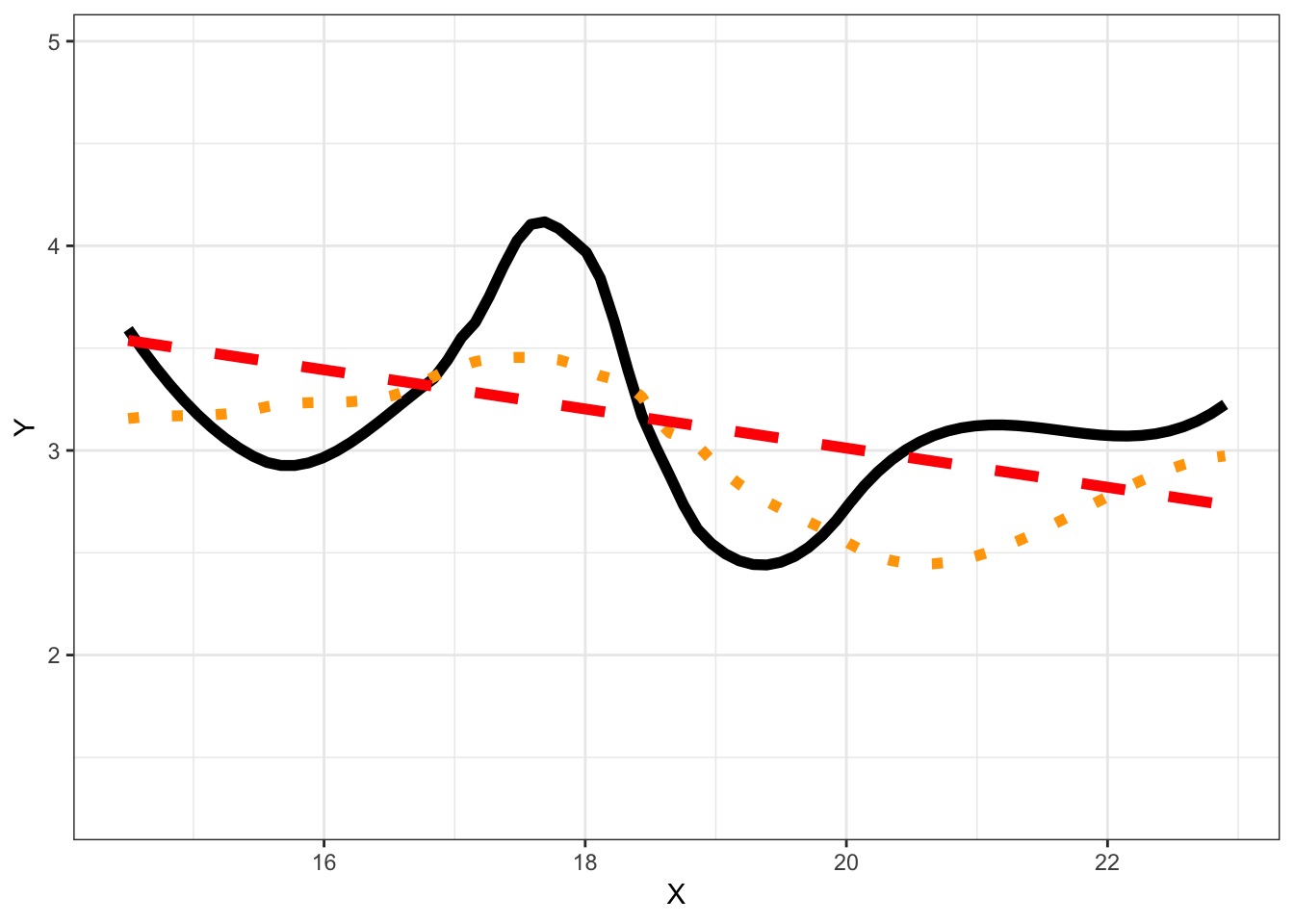
Information Loss and Kullback-Leibler Divergence

Information Loss(truth,model_i) = \(\mathscr{L}_{truth}log\frac{\mathscr{L}_{truth}}{\mathscr{L}_{model \thinspace i}}\)

Two neat properties:

1. Comparing Information Loss between model1 and model2, truth drops out as a constant!
   

2. We can therefore define a metric to compare Relative Information Loss

Defining an Information Criterion

Balancing General and Specific Truths

Which model better describes a general principle of how the world works?

How many parameters does it take to draw an elephant?

AIC

• AIC optimized for forecasting (out of sample deviance)
  
  
• Assumes large N relative to K
  • AICc for a correction
    
    

But Sample Size Can Influence Fit…

\[AIC = -2log(L(\theta | x)) + 2K\]

\[AICc = AIC + \frac{2K(K+1)}{n-K-1}K\]

AIC v. BIC

How can we Use AIC Values?

What causes species richness?

• Distance from fire patch
• Elevation
• Abiotic index
• Patch age
• Patch heterogeneity
• Severity of last fire
• Plant cover

Many Things may Influence Species Richness

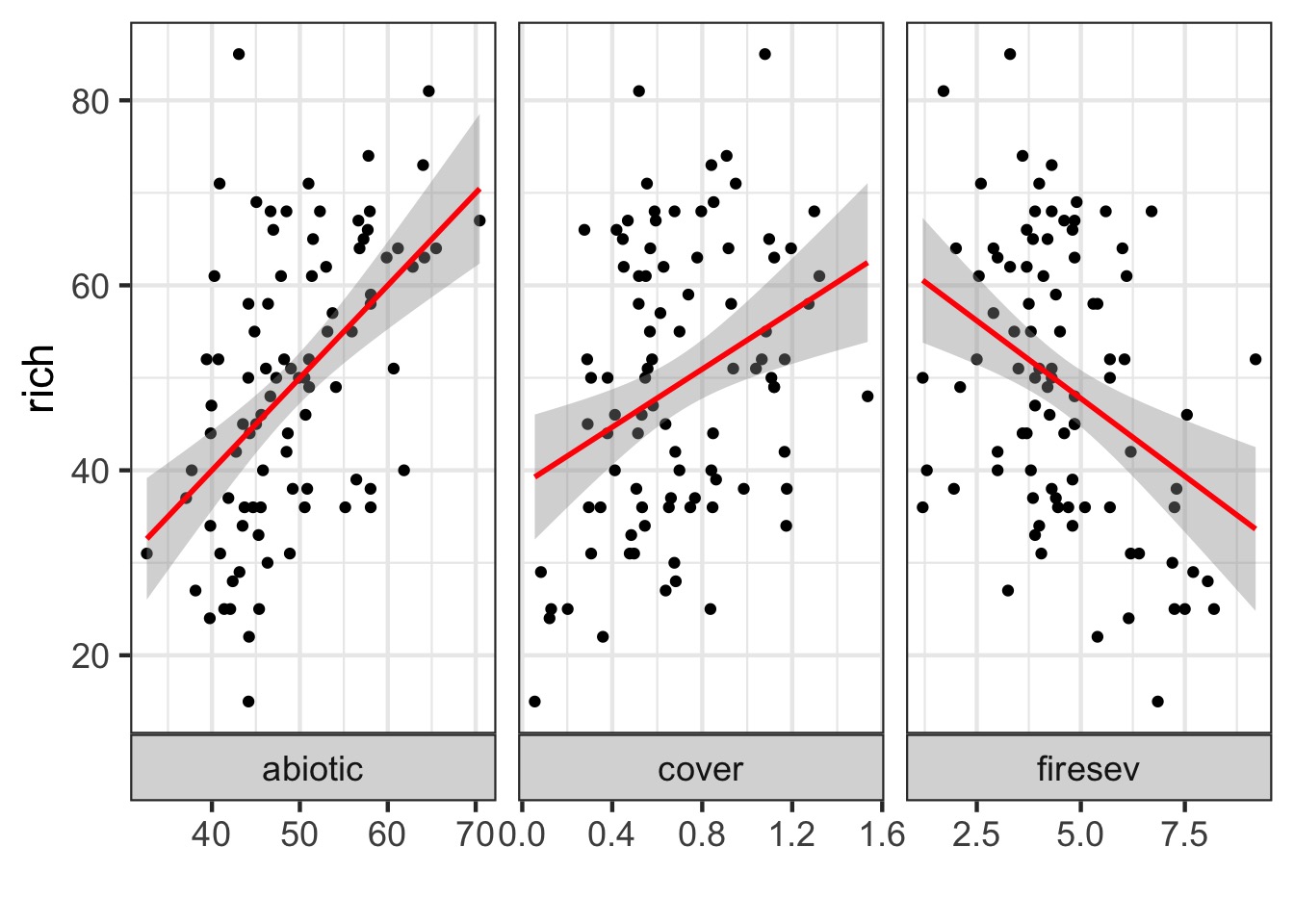
Implementing AIC: Create Models

k_abiotic <- lm(rich ~ abiotic, data=keeley)
  
k_firesev <- lm(rich ~ firesev, data=keeley)
  
k_cover <- lm(rich ~ cover, data=keeley)

Implementing AIC: Compare Models

AIC(k_abiotic)

[1] 722.2085

AIC(k_firesev)

[1] 736.0338

AIC(k_cover)

[1] 738.796

What if You Have a LOT of Potential Drivers?

7 models alone with 1 term each
127 possible without interactions.

A Quantitative Measure of Relative Support

\[w_{i} = \frac{e^{-\Delta_{i}/2 }}{\displaystyle \sum^R_{r=1} e^{-\Delta_{i}/2 }}\]
Where \(w_{i}\) is the relative support for model i compared to other models in the set being considered.

Model weights summed together = 1

Begin with a Full Model

keeley_full <- lm(rich ~  elev + abiotic + hetero +
                          distance + firesev + 
                          age + cover,
                  data = keeley)

Models with groups of variables

keeley_soil_fire <- lm(rich ~ elev + abiotic + hetero +
                          distance + firesev,
                  data = keeley)

keeley_plant_fire <- lm(rich ~  distance + firesev + 
                          age + cover,
                  data = keeley)

keeley_soil_plant <- lm(rich ~  elev + abiotic + hetero +
                          age + cover,
                  data = keeley)

One Factor Models

keeley_soil <- lm(rich ~  elev + abiotic + hetero,
                  data = keeley)

keeley_fire <- lm(rich ~  distance + firesev,
                  data = keeley)

keeley_plant <- lm(rich ~  age + cover,
                  data = keeley)

Null Model

keeley_null <- lm(rich ~  1,
                  data = keeley)

Now Compare Models Weights

So, I have some sense of good models? What now?

Variable Weights

How to I evaluate the importance of a variable?

Variable Weight = sum of all weights of all models including a variable. Relative support for inclusion of parameter in models.

Importance values of 'firesev':

w+ (models including parameter): 0.99 
w- (models excluding parameter): 0.01 

Model Averaged Parameters

\[\hat{\bar{\beta}} = \frac{\sum w_{i}\hat\beta_{i}}{\sum{w_i}}\]

\[var(\hat{\bar{\beta}}) = \left [ w_{i} \sqrt{var(\hat\beta_{i}) + (\hat\beta_{i}-\hat{\bar{\beta_{i}}})^2} \right ]^2\]
Buckland et al. 1997

Model Averaged Parameters

Multimodel inference on "firesev" based on AICc

AICc table used to obtain model-averaged estimate with shrinkage:

           K   AICc Delta_AICc AICcWt Estimate   SE
full       9 688.16       0.00   0.89    -1.02 0.80
plant_fire 6 709.69      21.53   0.00    -1.39 0.92
soil_fire  7 692.55       4.39   0.10    -1.89 0.73
soil_plant 7 696.57       8.41   0.01     0.00 0.00
soil       5 711.73      23.56   0.00     0.00 0.00
plant      4 737.16      49.00   0.00     0.00 0.00
fire       4 707.49      19.33   0.00    -2.03 0.80
null       2 747.25      59.09   0.00     0.00 0.00

Model-averaged estimate with shrinkage: -1.09 
Unconditional SE: 0.84 
95% Unconditional confidence interval: -2.74, 0.56

Model Averaged Predictions

newData <- data.frame(distance = 50,
                      elev = 400,
                      abiotic = 48,
                      age = 2,
                      hetero = 0.5,
                      firesev = 10,
                      cover=0.4)

Model-averaged predictions on the response scale
based on entire model set and 95% confidence interval:

  mod.avg.pred uncond.se lower.CL upper.CL
1       31.666     6.136    19.64   43.692

Death to single models!

• While sometimes the model you should use is clear, more often it is not
  
  
• Further, you made those models for a reason: you suspect those terms are important
  
  
• Better to look at coefficients across models
  
  
• For actual predictions, ensemble predictions provide real uncertainty

Ensemble Prediction

• Ensemble prediction gives us better uncertainty estimates
  
  
• Takes relative weights of predictions into account
  
  
• Takes weights of coefficients into account
  
  
• Basicaly, get simulated predicted values, multiply them by model weight

What about IC Analyses in Bayes?

Can we just use AIC?

• We do estimate the posterior distribution of the deviance
  
  
• Average of the posterior, \(\bar{D}\) is our \(D_{train}\)
  
  
• But what about # of parameters?
  • With flat priors, it’s just the # of params!
    
  • But once priors are not flat, we are using additional information
    
  • It is as if we have fewer parameters to estimate, so AIC becomes problematic

So how do we maximize prediction?

• Why not look at the pieces that make up the deviance
  • The pointwise predictive power of the posterior
    
    
• We can define the Pr(y_i | posterior simulations)
  • This tells us the distribution of the predictive power of our posterior for each point
    
    
• \(llpd = \sum log Pr(y_i | \theta)\)

But what about Parameters?

• We know that as k increases, our uncertainty in coefficients increases
  • And priors shrink uncertainty when good
    
    
• Uncertainty is reflected in the distribution of Pr(y_i | simulations)
  
  
• Thus, this variance gives us an effective penalty term
  
  
• \(p_{waic} = \sum Var(log Pr(y_i | \theta))\)

Widely Applicable IC

WAIC with Cover Only Model

WAIC(k_cover_brm)

Computed from 4000 by 90 log-likelihood matrix

          Estimate   SE
elpd_waic   -369.2  5.1
p_waic         2.5  0.4
waic         738.4 10.1

WAIC Across All Models

We Can Weight

The Futility of Model Selection in a Bayesian World

Are these really different?

The Futility of Model Selection in a Bayesian World

# A tibble: 55 x 3
   Model                                  WAIC    SE
   <chr>                                 <dbl> <dbl>
 1 k_abiotic_brm - k_cover_brm           -16.2 12.2 
 2 k_abiotic_brm - k_firesev_brm         -13.6 11.6 
 3 k_abiotic_brm - keeley_full_brm        35.7 11.3 
 4 k_abiotic_brm - keeley_soil_fire_brm   30.8 10.5 
 5 k_abiotic_brm - keeley_plant_fire_brm  13.6 12.4 
 6 k_abiotic_brm - keeley_soil_plant_brm  26.7  9.70
 7 k_abiotic_brm - keeley_soil_brm        11.0  6.28
 8 k_abiotic_brm - keeley_fire_brm        15.2 11.7 
 9 k_abiotic_brm - keeley_plant_brm      -13.7 11.9 
10 k_abiotic_brm - keeley_null_brm       -24.7 10.2 
# ... with 45 more rows

Maybe average coefficients?

Model Averaged Coefficients

Model Averaged Coefficients

• Draw values from posterior of each model with frequency porportional to model weight

Embracing Full Uncertainty

• Current controversy over meaning of coefficient weights (even with AIC)
  
  
• In a Bayesian worldview, we want to embrace uncertainty!
  • Look at weighted predictions over all models
    
  • Weights determine probability of drawing from a model’s posterior
    
    
• So, ensemble predictions marginalizing over variables not of interest

Ensemble Predictions

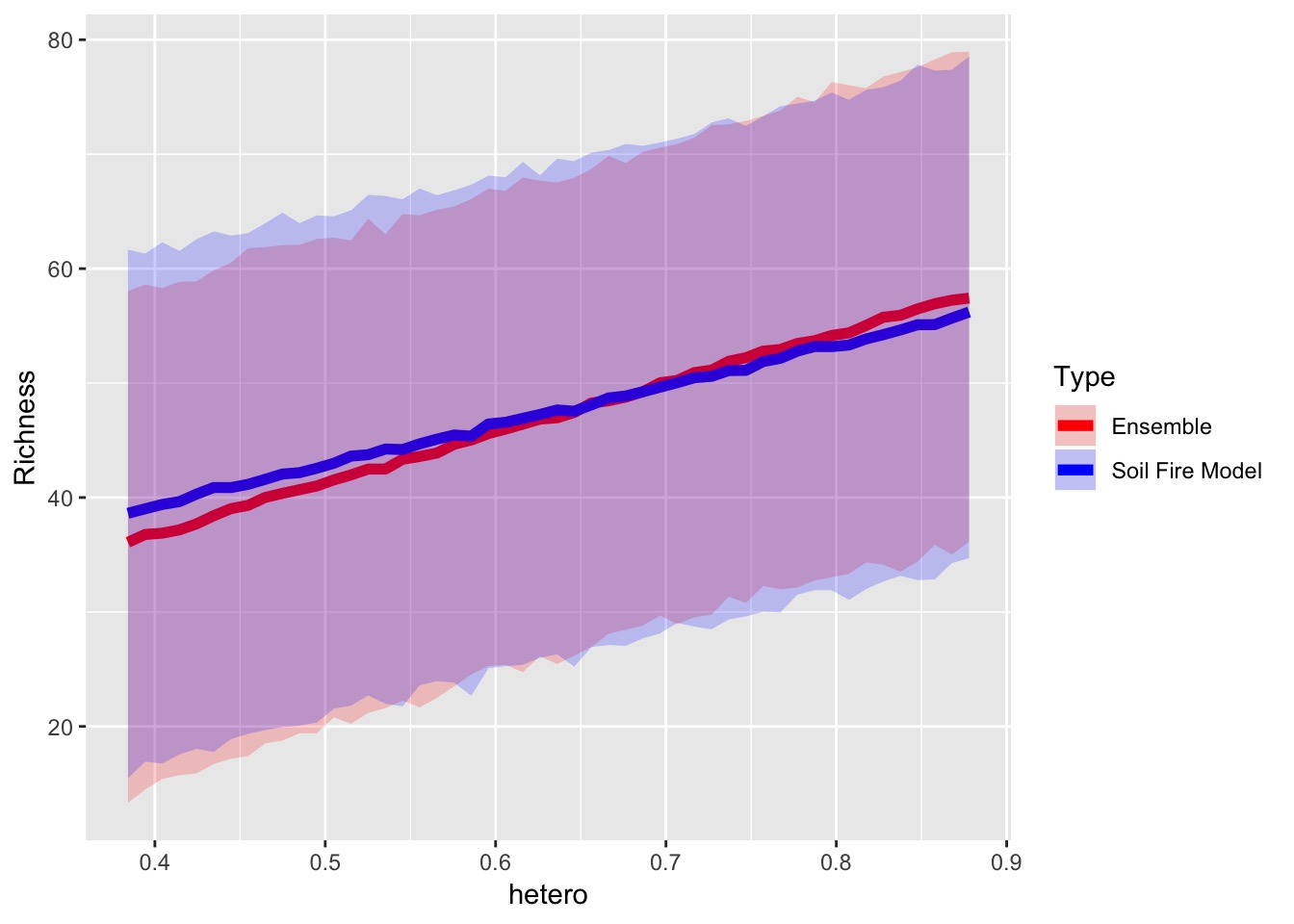
Final Notes

• IC analyses aid in model selection. One must still evaluate parameters and parameter error.
  
  
• Your inferences are constrained solely to the range of models you consider. You may have missed the ’best’ model.
  
  
• All inferences MUST be based on a priori models. Post-hoc model dredging could result in an erroneous ’best’ model suited to your unique data set.
  
  
• Ensemble predictions are a powerful practice to show true unertainty