Bayesian Statistics: an introduction

image

Deriving Truth from Data

  • Frequentist Inference: Correct conclusion drawn from repeated experiments
    • Uses p-values and CIs as inferential engine

  • Likelihoodist Inference: Evaluate the weight of evidence for different hypotheses
    • Derivative of frequentist mode of thinking
    • Uses model comparison (sometimes with p-values…)

  • Bayesian Inference: Probability of belief that is constantly updated
    • Uses explicit statements of probability and degree of belief for inferences

Similarities in Frequentist and Likelihoodist Inference

  • Frequentist inference with Linear Models

    • Estimate ’true’ slope and intercept

    • State confidence in our estimate

    • Evaluate probabilty of obtaining data or more extreme data given a hypothesis

  • Likelihood inference with Linear Models

    • Estimate ’true’ slope and intercept

    • State confidence in our estimate

    • Evaluate likelihood of data versus likelihood of alternate hypothesis

Bayesian Inference

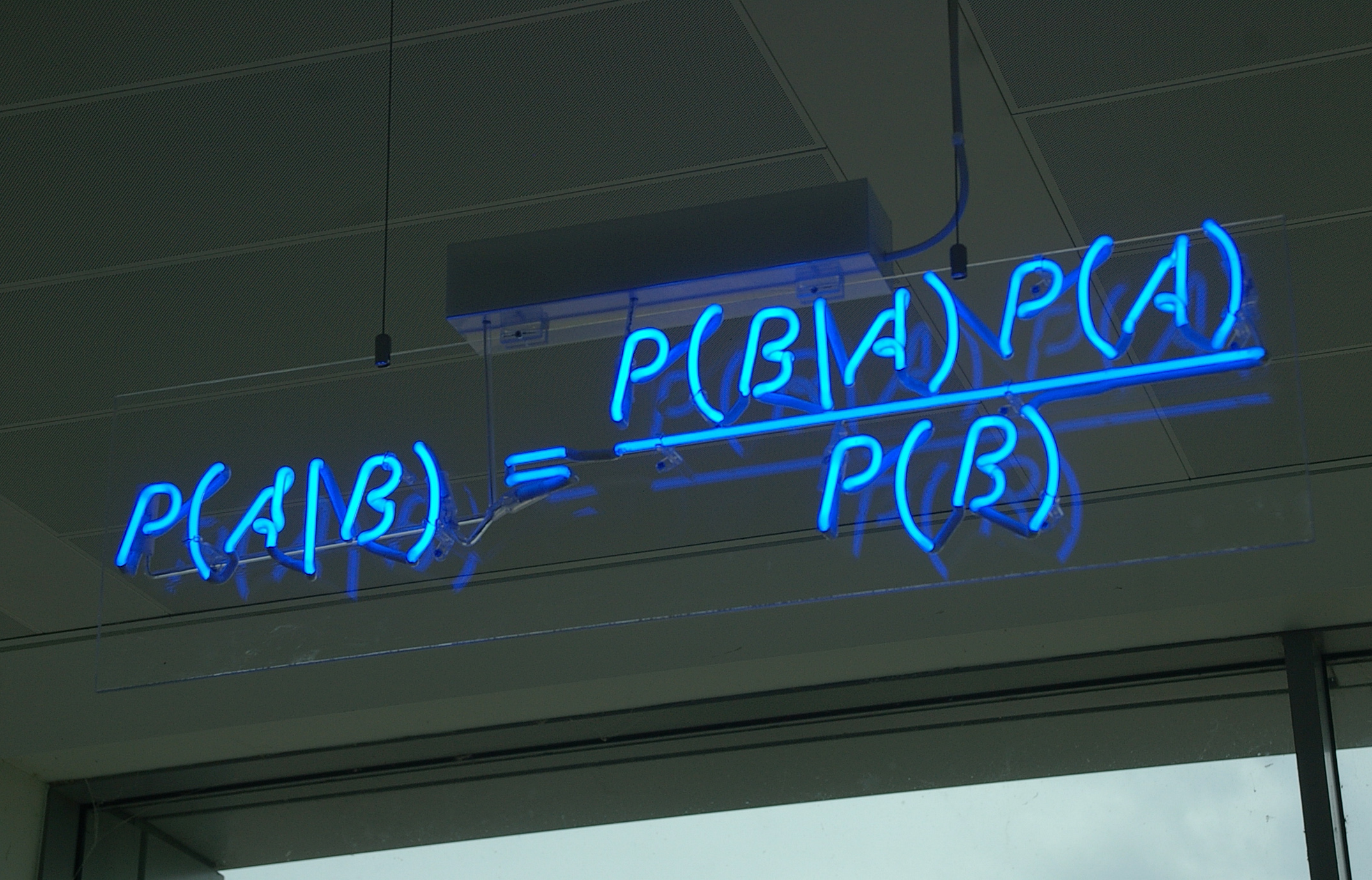
image

  • Estimate probability of a parameter

  • State degree of believe in specific parameter values

  • Evaluate probability of hypothesis given the data

  • Incorporate prior knowledge

  • Frequentist: p(x ≤ D | H)


  • Likelhoodist: p( D | H)


  • p(H | D)

Why is p(H | D) awesome?

  • Up until now we have never thought about the probability of a hypothesis

  • The probability data (or more extreme data) given a hypothesis provides an answer about a single point hypothesis

  • We have been unable to talk about the probability of different hypotheses (or parameter values) relative to one another

  • p(H | D) results naturally from Bayes Theorey

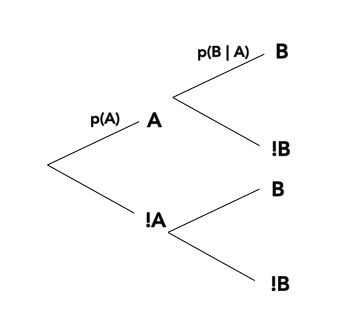
Bayes Theorem

We know…

\[\huge p(a\ and\ b) = p(a)p(b|a)\]

Bayes Theorem

And Also…

\[\huge p(a\ and\ b) = p(b)p(a|b)\]

as \(p(b) = p(b+a)+p(b|!a)\)

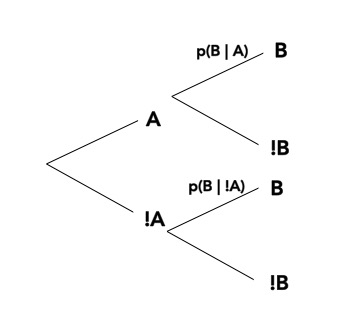
Bayes Theorem

And so…

\[\huge p(a)p(b|a) = p(b)p(a|b) \]

Bayes Theorem

And thus…

\[\huge p(a|b) = \frac{p(b|a)p(a)}{p(b)} \]

Bayes Theorem and Data



\[\huge p(H|D) = \frac{p(D|H)p(H)}{p(D)} \]

where p(H|D) is your posterior probability of a hypothesis

What is a posterior distribution?

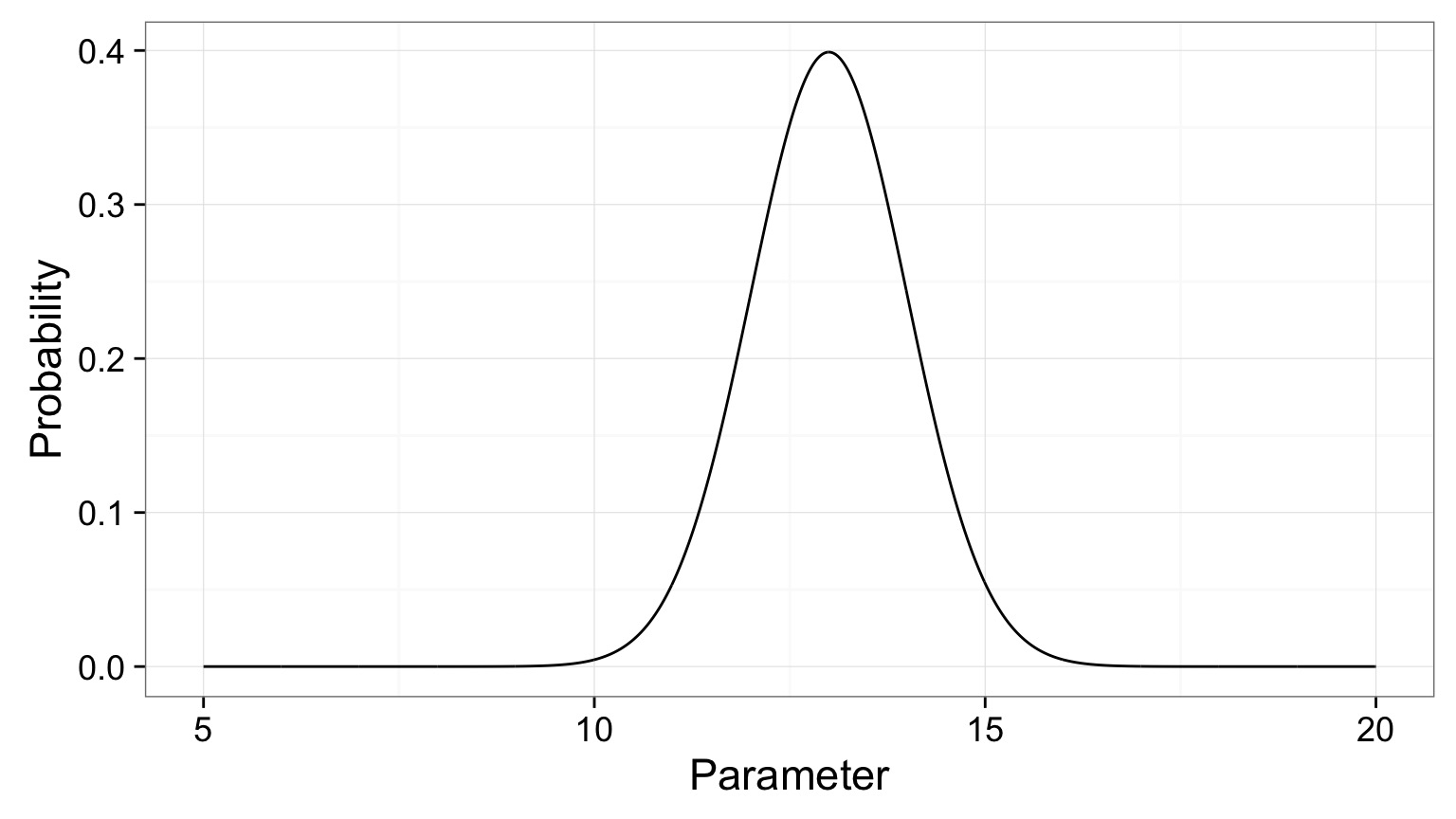
What is a posterior distribution?

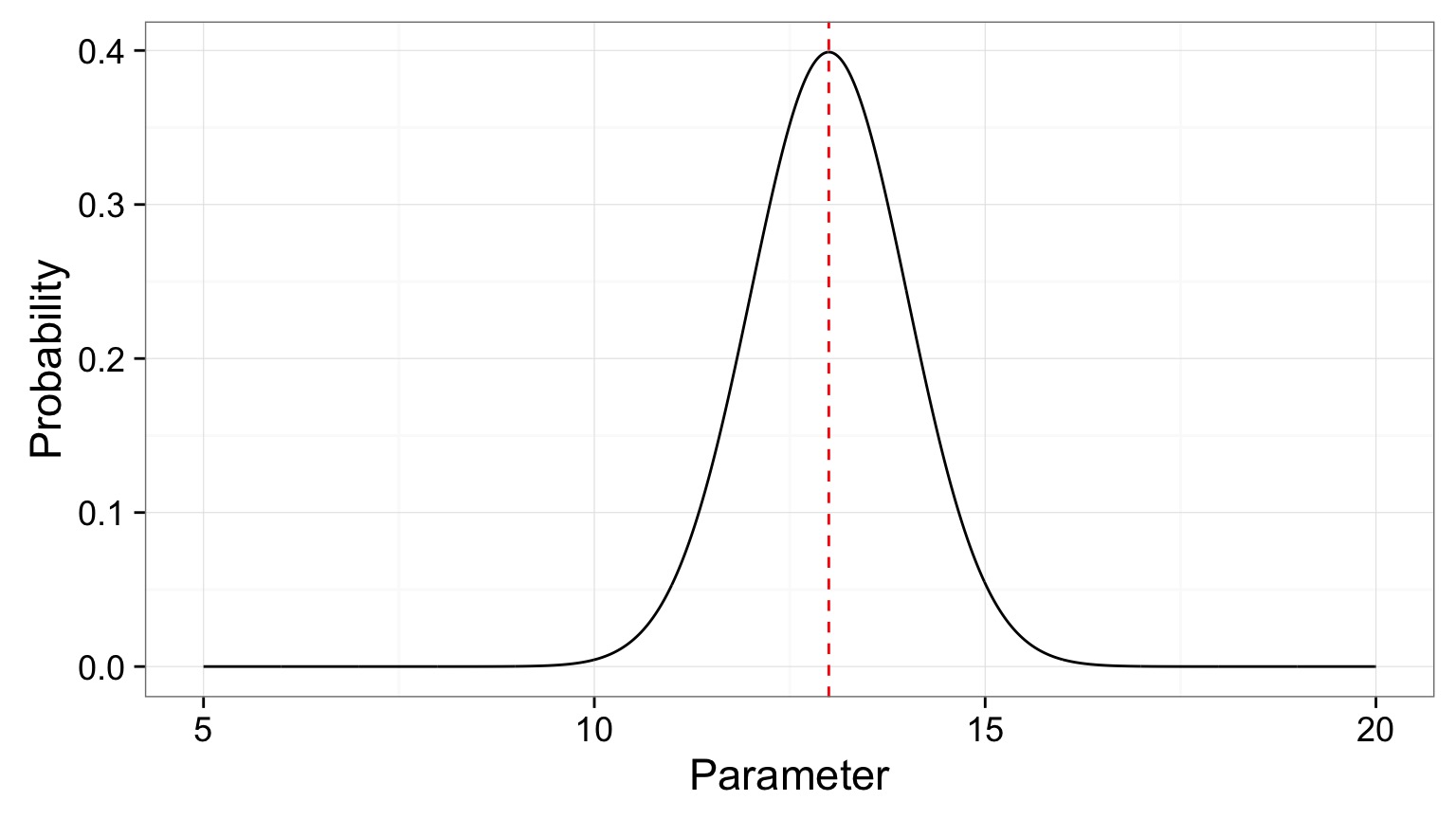
The probability that the parameter is 13 is 0.4

What is a posterior distribution?

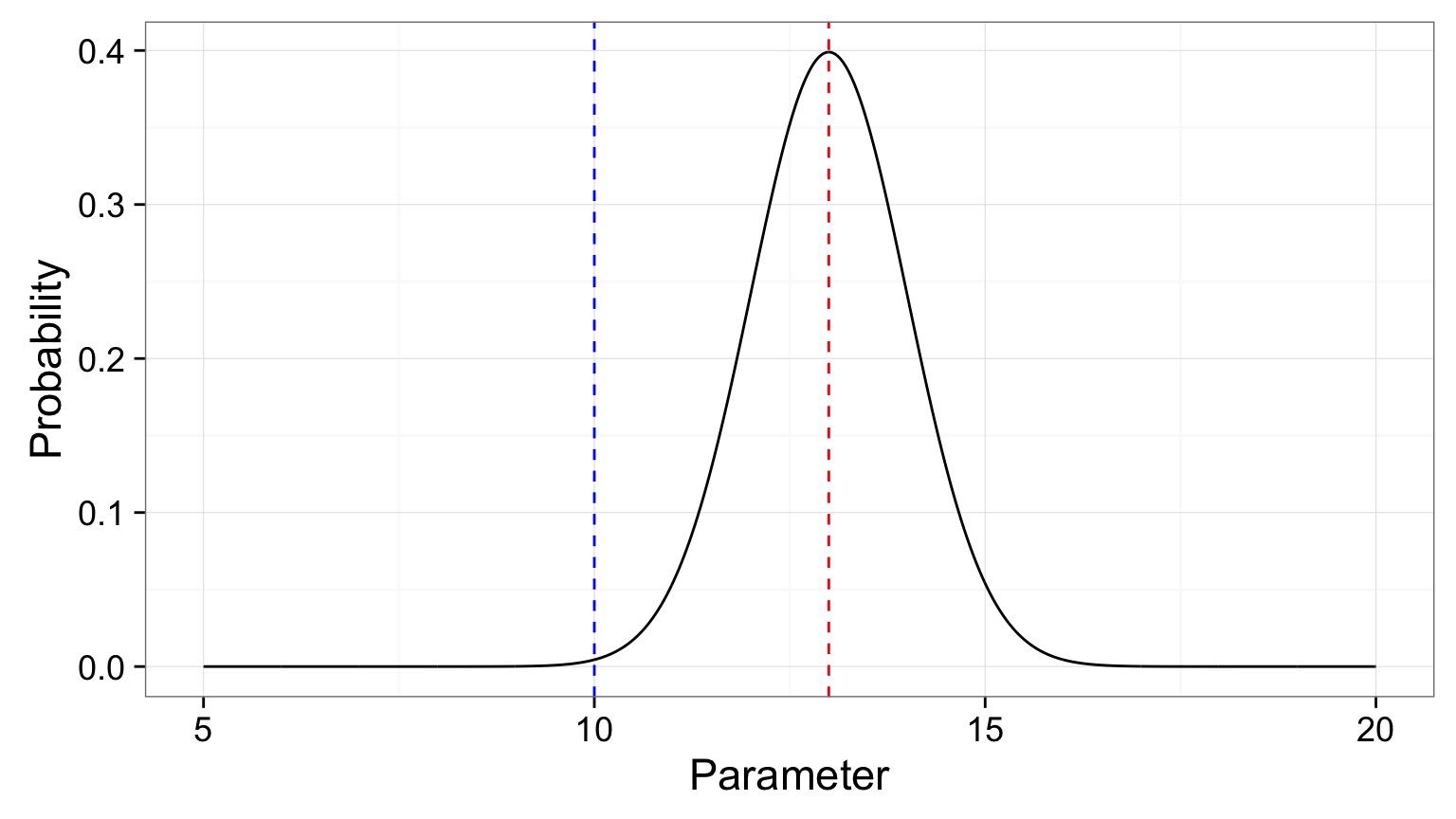
The probability that the parameter is 13 is 0.4 The probability that the parameter is 10 is 0.044

What is a posterior distribution?

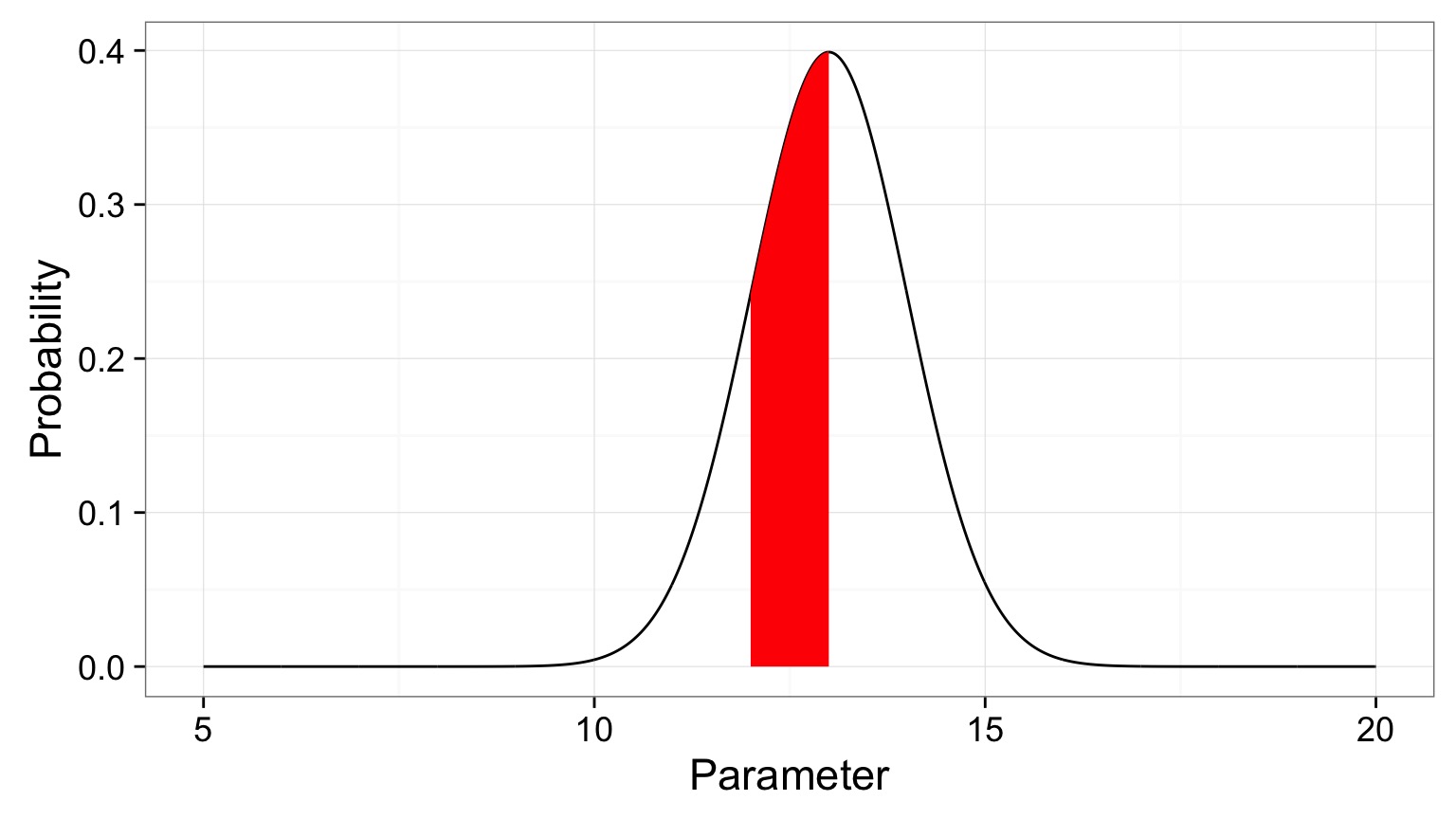
Probability that parameter is between 12 and 13 = 0.3445473

Bayesian Credible Interval

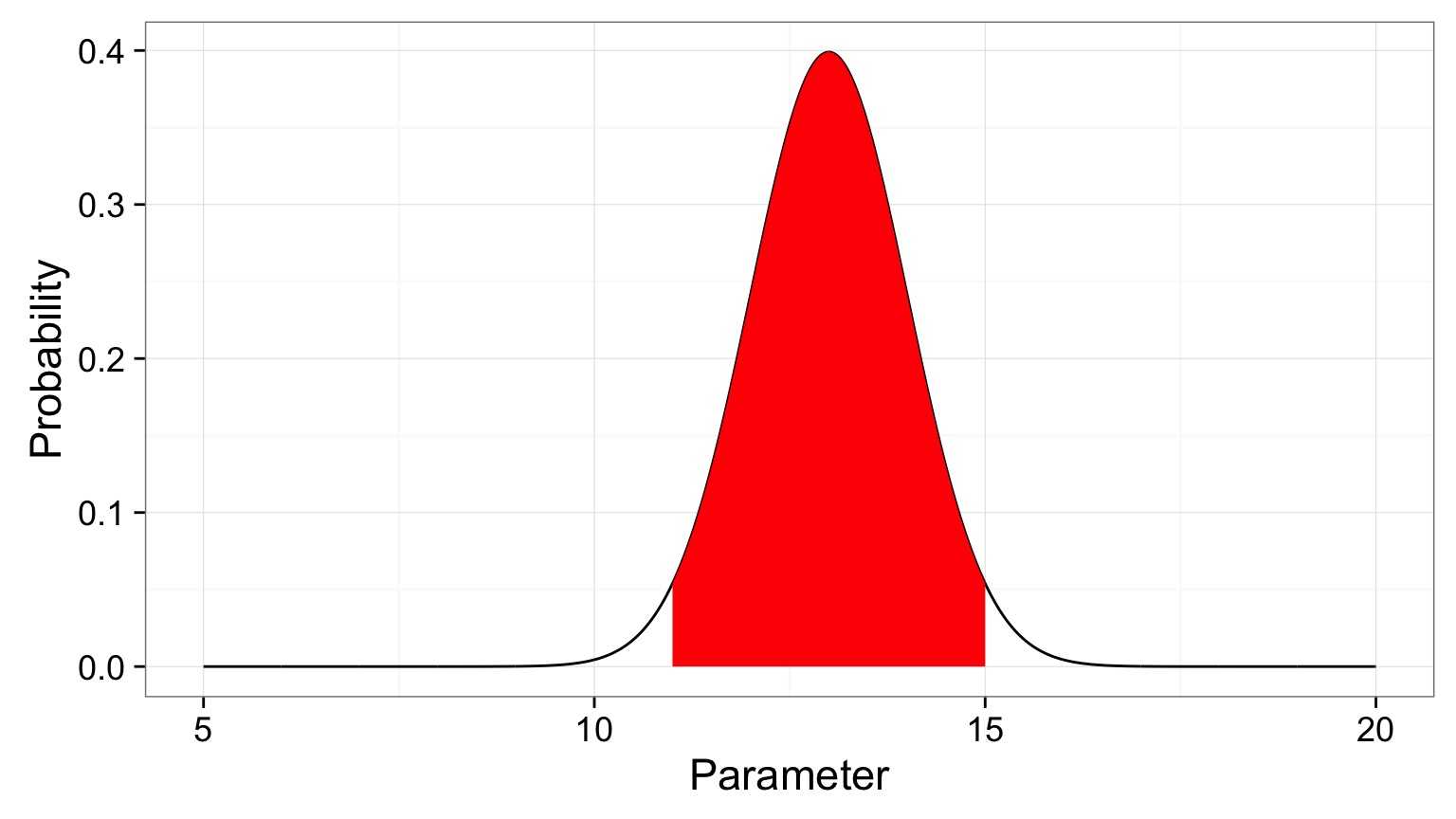
Area that contains 95% of the probability mass of the posterior distribution

Evaluation of a Posterior: Bayesian Credible Intervals

In Bayesian analyses, the 95% Credible Interval is the region in which we find 95% of the possible parameter values. The observed parameter is drawn from this distribution. For normally distributed parameters:

\[\hat{\beta} - 2*\hat{SD} \le \hat{\beta} \le \hat{\beta} +2*\hat{SD}\]

where \(\hat{SD}\) is the SD of the posterior distribution of the parameter \(\beta\). Note, for non-normal posteriors, the distribution may be different.

Evaluation of a Posterior: Frequentist Confidence Intervals

In Frequentist analyses, the 95% Confidence Interval of a parameter is the region in which, were we to repeat the experiment an infinite number of times, the true value would occur 95% of the time. For normal distributions of parameters:



\[\hat{\beta} - t(\alpha, df)SE_{\beta} \le \beta \le \hat{\beta} +t(\alpha, df)SE_{\beta}\]

Credible Intervals versus Confidence Intervals

  • Frequentist Confidence Intervals tell you the region you have confidence a true value of a parameter may occur

  • If you have an estimate of 5 with a Frequentist CI of 2, you cannot say how likely it is that the parameter is 3, 4, 5, 6, or 7

  • Bayesian Credible Intervals tell you the region that you have some probability of a parameter value

  • With an estimate of 5 and a CI of 2, you can make statements about degree of belief in whether a parmeter is 3, 4,5, 6 or 7 - or even the probability that it falls outside of those bounds

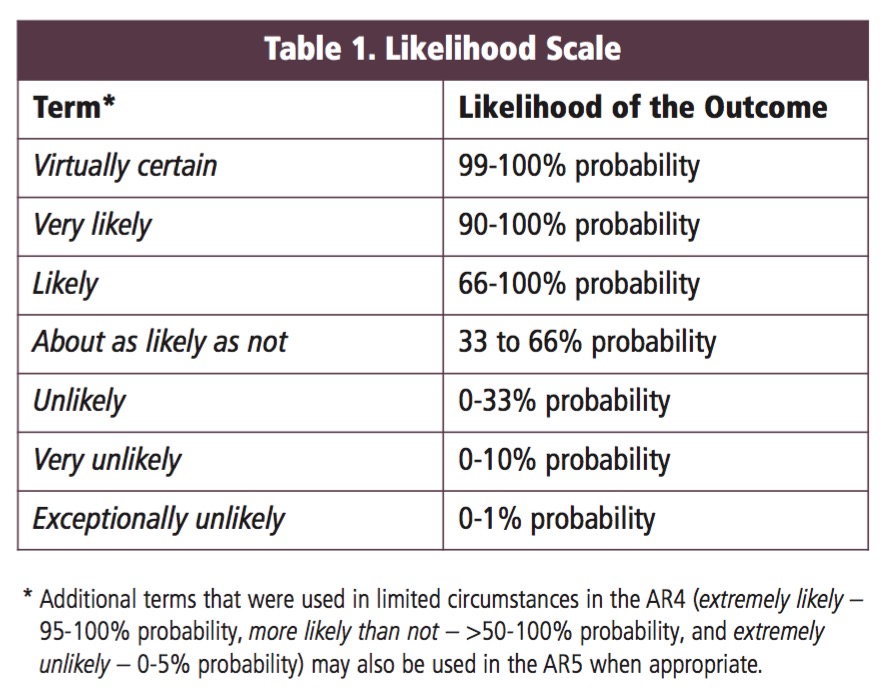
Degree of believe in a result

You can discuss the probability that your parameter is opposite in sign to its posterior modal estimate. This yields a degree of belief that you at least have the sign correct (i.e., belief in observing a non-zero value)

Talking about Uncertainty the IPCC Way

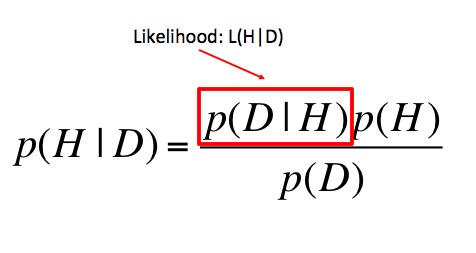
What are the other parts of Bayes Theorem?



\[\huge p(H|D) = \frac{p(D|H)p(H)}{p(D)} \]

where p(H|D) is your posterior probability of a hypothesis

Hello Again, Likelihood

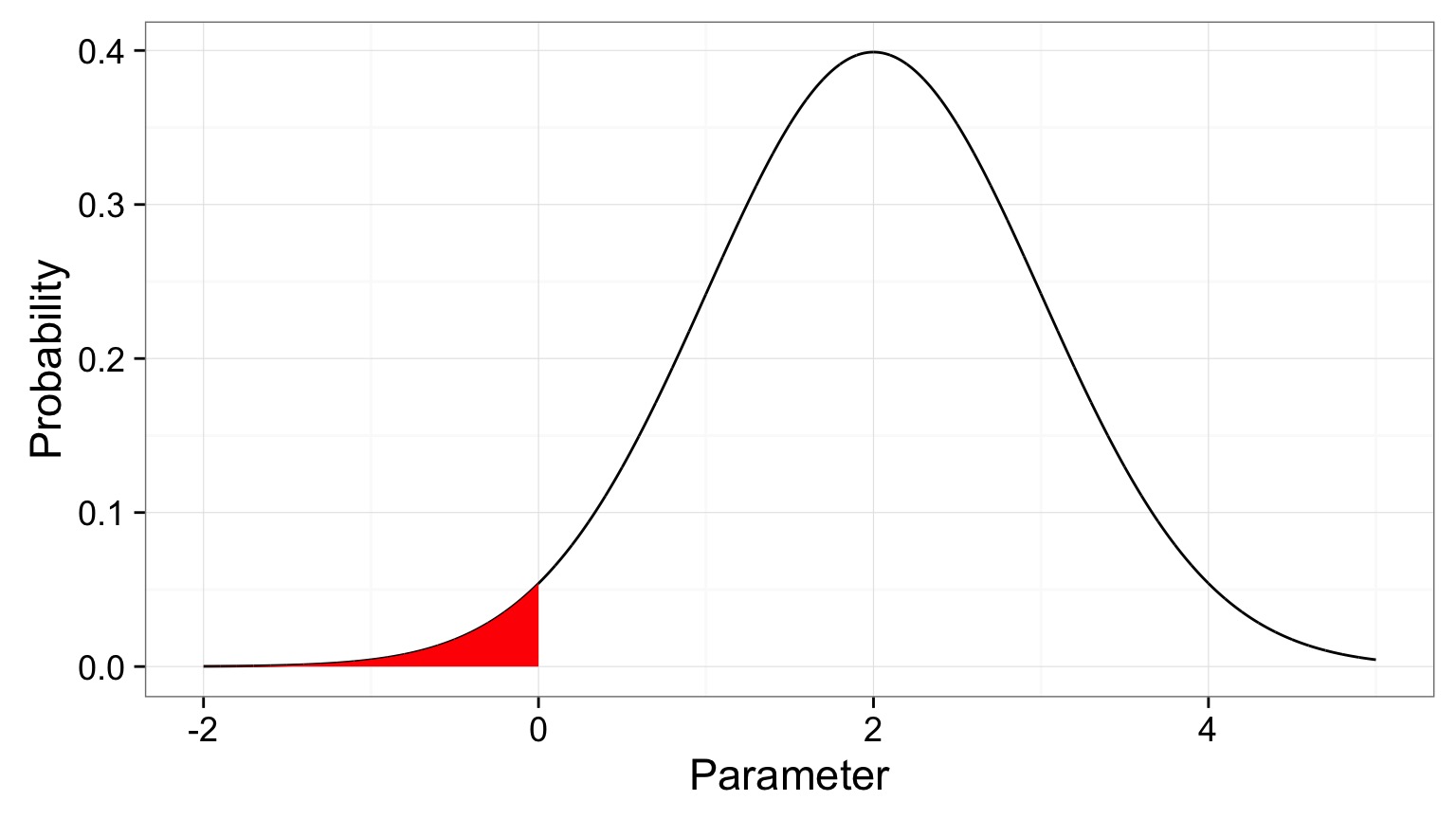
Prior Probability



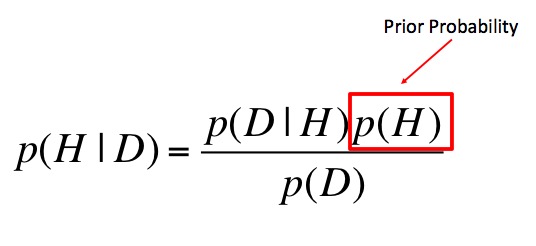
This is why Bayes is different from Likelihood!</span

How do we Choose a Prior?

  • A prior is a powerful tool, but it can also influence our results of chosen poorly. This is a highly debated topic.

  • Conjugate priors make some forms of Bayes Theorem analytically solveable

  • If we have objective prior information - from pilot studies or the literature - we can use it to obtain a more informative posterior distribution

  • If we do not, we can use a weak or flat prior (e.g., N(0,1000)). Note: constraining the range of possible values can still be weakly informative - and in some cases beneficial

The Influence of Priors

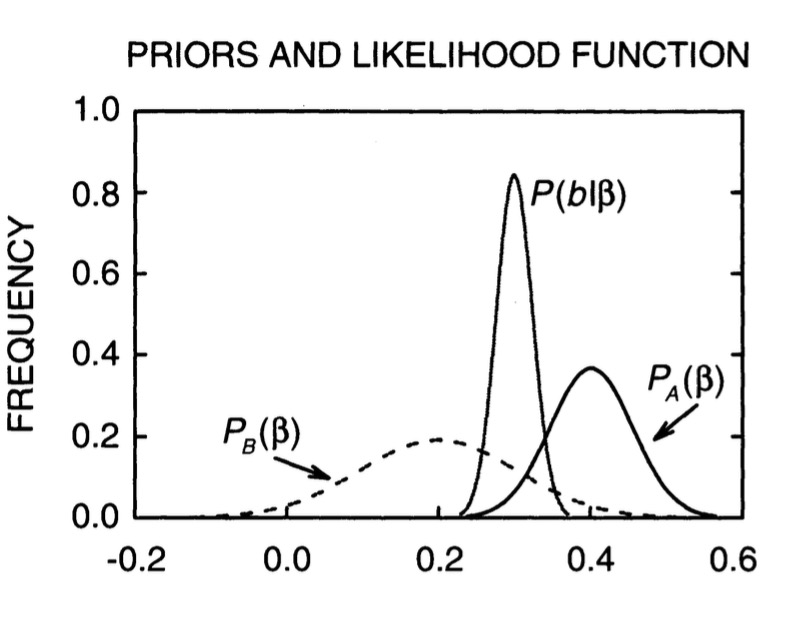
The Influence of Priors

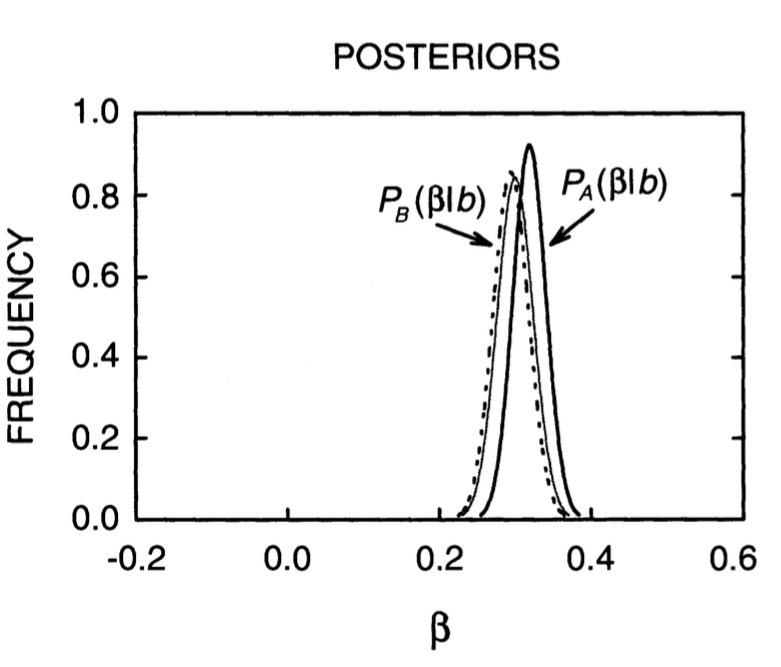
Priors and Sample Size

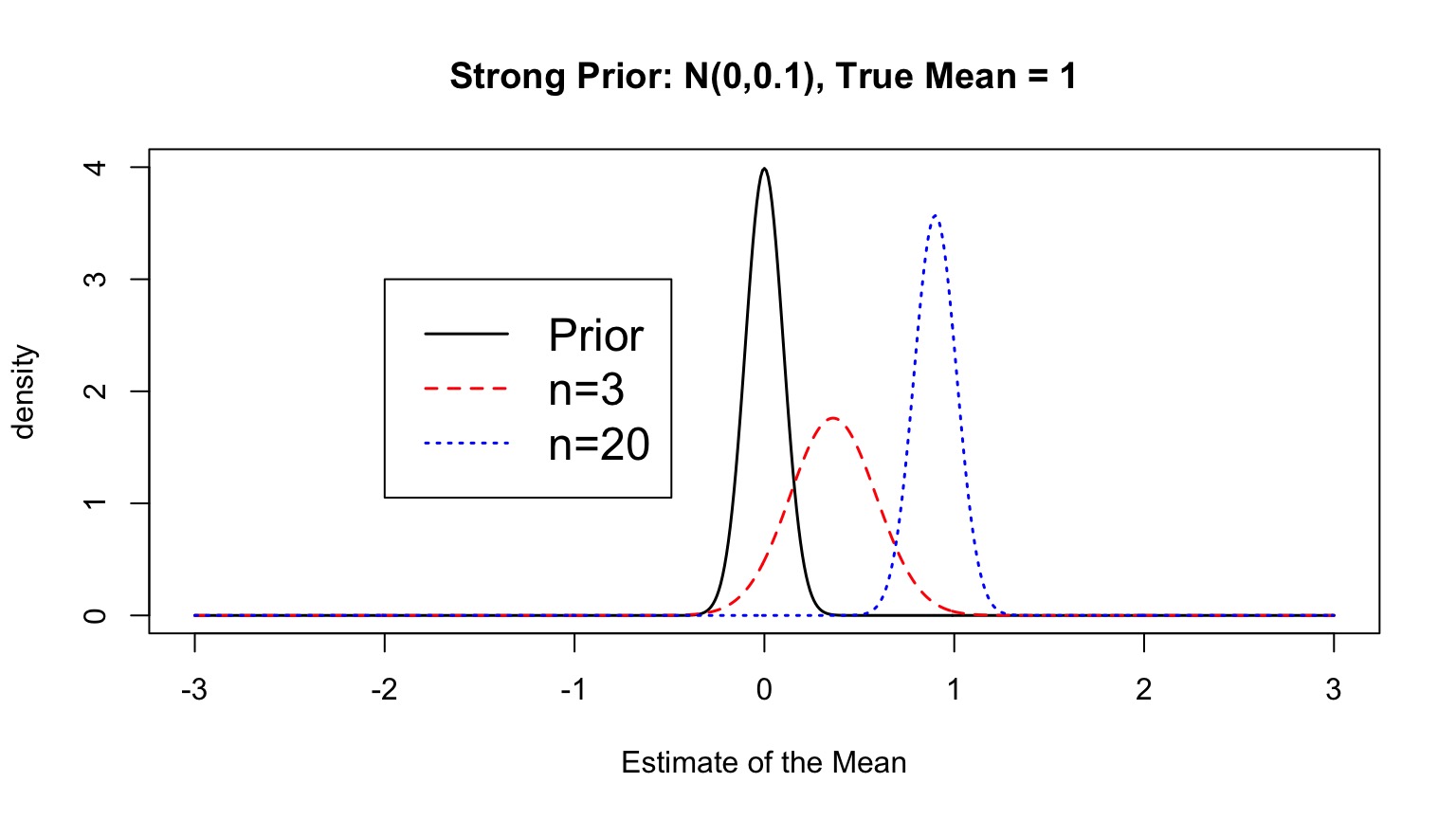
p(data) is just a big summation/integral

Denominator: The Marginal Distribution


Essentially, all alternate hypotheses

Denominator - marginal distribution - becomes an integral of likelihoods if \(B\) is continuous - i.e. fitting a particular parameter value. It normalizes the equation to be between 0 and 1.

Bayes Theorem in Action

image

http://xkcd.com/1132/

Bayes Theorem in Action

\[p(Sun Explodes | Yes) = \frac{p(Yes | Sun Explodes)p(Sun Explodes)}{p(Yes)}\]

We know/assume:
p(Sun Explodes) = 0.0001, P(Yes \(|\) Sun Explodes) = 35/36

So…
p(Yes) = P(Yes \(|\) Sun Explodes)p(Sun Explodes)
= 35/36 * 0.0001
= 9.7e10^-5



credit: Amelia Hoover

Bayes Theorem in Action

\[p(Sun Explodes | Yes) = \frac{p(Yes | Sun Explodes)p(Sun Explodes)}{p(Yes)}\]

We can calculate:
p(Yes) = P(Yes \(|\) Sun Explodes)p(Sun Explodes) +
    P(Yes \(|\) Sun Doesn’t Explode)p(Sun Doesn’t Explodes)

= 35/36 * 0.0001 + 1/36 * 0.9999

= 0.0277775




credit: Amelia Hoover

Bayes Theorem in Action

\[p(Sun Explodes | Yes) = \frac{p(Yes | Sun Explodes)p(Sun Explodes)}{p(Yes)}\]

\[p(Sun Explodes | Yes) = \frac{0.0001*35/36}{0.028}\] \[= 0.0035\]
Incorporating Prior Information about the Sun Exploding gives us a very different answer


Note, we can also evaluate the probability of the alternate hypothesis - p(Sun Doesn’t Explode \(|\) Yes)

Where have we gone?



Ellison 1996