Fitting Models with Likelihood!
Outline
- Review of Likelihood
- Comparing Models with Likelihood
- Linear Regression with Likelihood
Deriving Truth from Data
- Frequentist Inference: Correct conclusion drawn from repeated experiments
- Uses p-values and CIs as inferential engine
- Uses p-values and CIs as inferential engine
- Likelihoodist Inference: Evaluate the weight of evidence for different hypotheses
- Derivative of frequentist mode of thinking
- Uses model comparison (sometimes with p-values…)
- Derivative of frequentist mode of thinking
- Bayesian Inference: Probability of belief that is constantly updated
- Uses explicit statements of probability and degree of belief for inferences
Likelihood: how well data support a given hypothesis.
Note: Each and every parameter choice IS a hypothesis
Likelihood Defined
\[\Large L(H | D) = p(D | H)\]
Where the D is the data and H is the hypothesis (model) including a both a data generating process with some choice of parameters (aften called \(\theta\)). The error generating process is inherent in the choice of probability distribution used for calculation.
Example of Maximum Likelihood Fit
Let’s say we have counted 10 individuals in a plot. Given that the population is Poisson distributed, what is the value of \(\lambda\)?
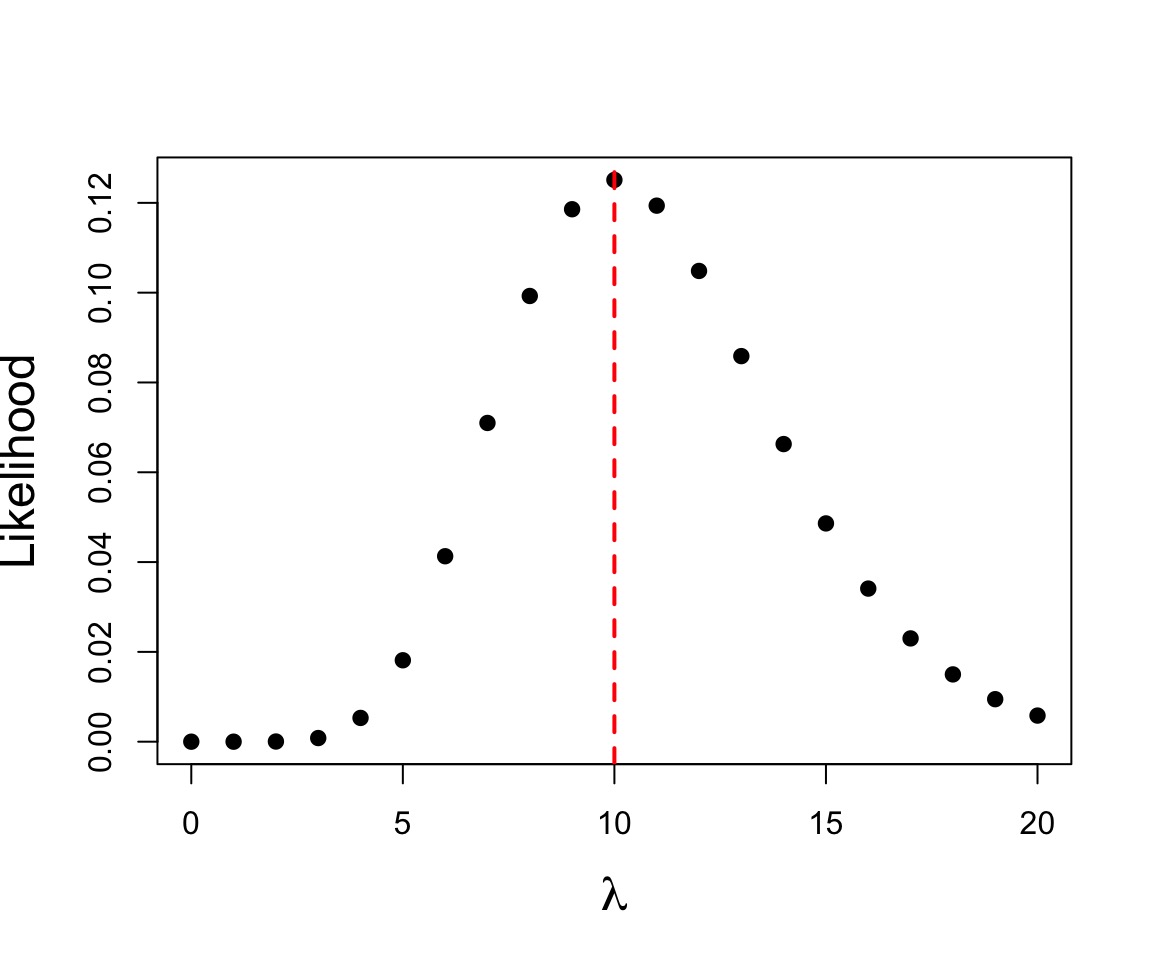
$$p(x) = \frac{\lambda^{x}e^{-\lambda}}{x!}$$
where we search all possible values of λ
Likelihood Function
\[\Large p(x) = \frac{\lambda^{x}e^{-\lambda}}{x!}\]
- This is a Likelihood Function for one sample
- It is the Poisson Probability Density function
- \(Dpois = \frac{\lambda^{x}e^{-\lambda}}{x!}\)
What is the probability of the data given the parameter?
p(a and b) = p(a)p(b)
$$p(D | \theta) = \prod_{i=1}^n p(d_{i} | \theta)$$
$$ = \prod_{i=1}^n \frac{\theta^{x_i}e^{-\theta}}{x_!}$$
Outline
- Review of Likelihood
- Comparing Models with Likelihood
- Linear Regression with Likelihood
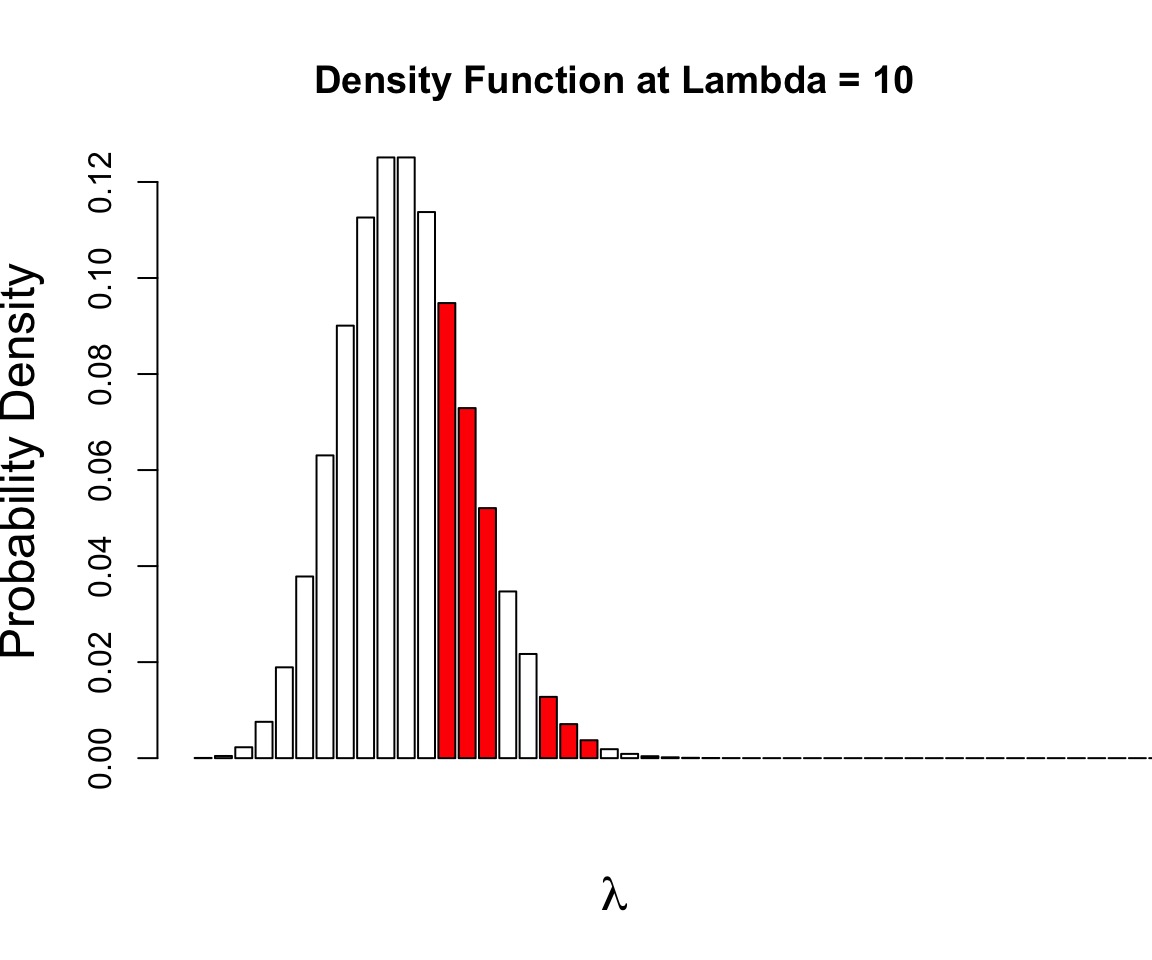
Can Compare p(data | H) for alternate Parameter Values
Compare \(p(D|\theta_{1})\) versus \(p(D|\theta_{2})\)
Likelihood Ratios
\[\LARGE G = \frac{L(H_1 | D)}{L(H_2 | D)}\]
- G is the ratio of Maximum Likelihoods from each model
- Used to compare goodness of fit of different models/hypotheses
- Most often, \(\theta\) = MLE versus \(\theta\) = 0
- \(-2 log(G)\) is \(\chi^2\) distributed
Likelihood Ratio Test
- A new test statistic: \(D = -2 log(G)\)
- \(= 2 [Log(L(H_2 | D)) - Log(L(H_1 | D))]\)
- It’s \(\chi^2\) distributed!
- DF = Difference in # of Parameters
- DF = Difference in # of Parameters
- If \(H_1\) is the Null Model, we have support for our alternate model
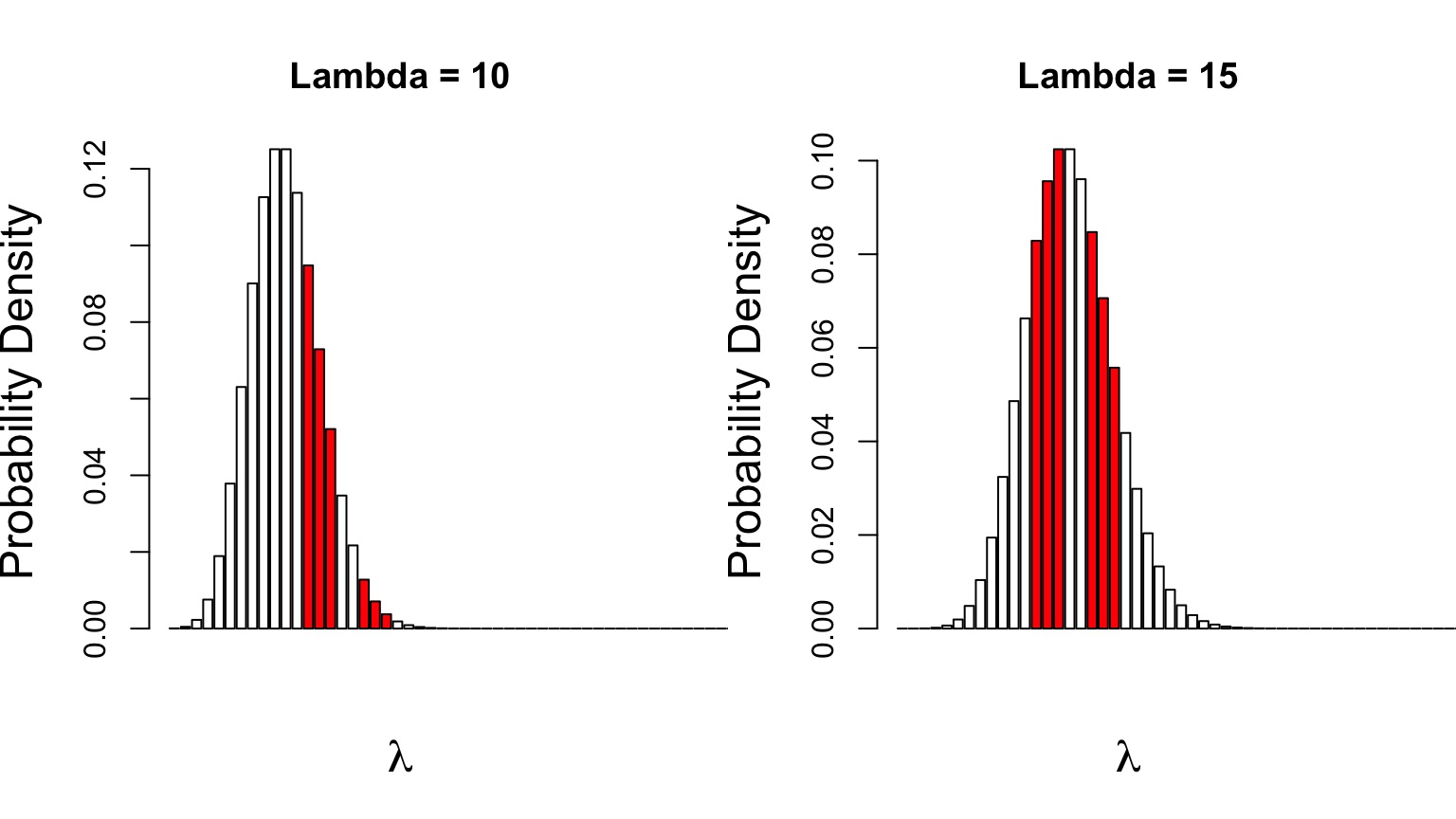
Likelihood Ratio at Work
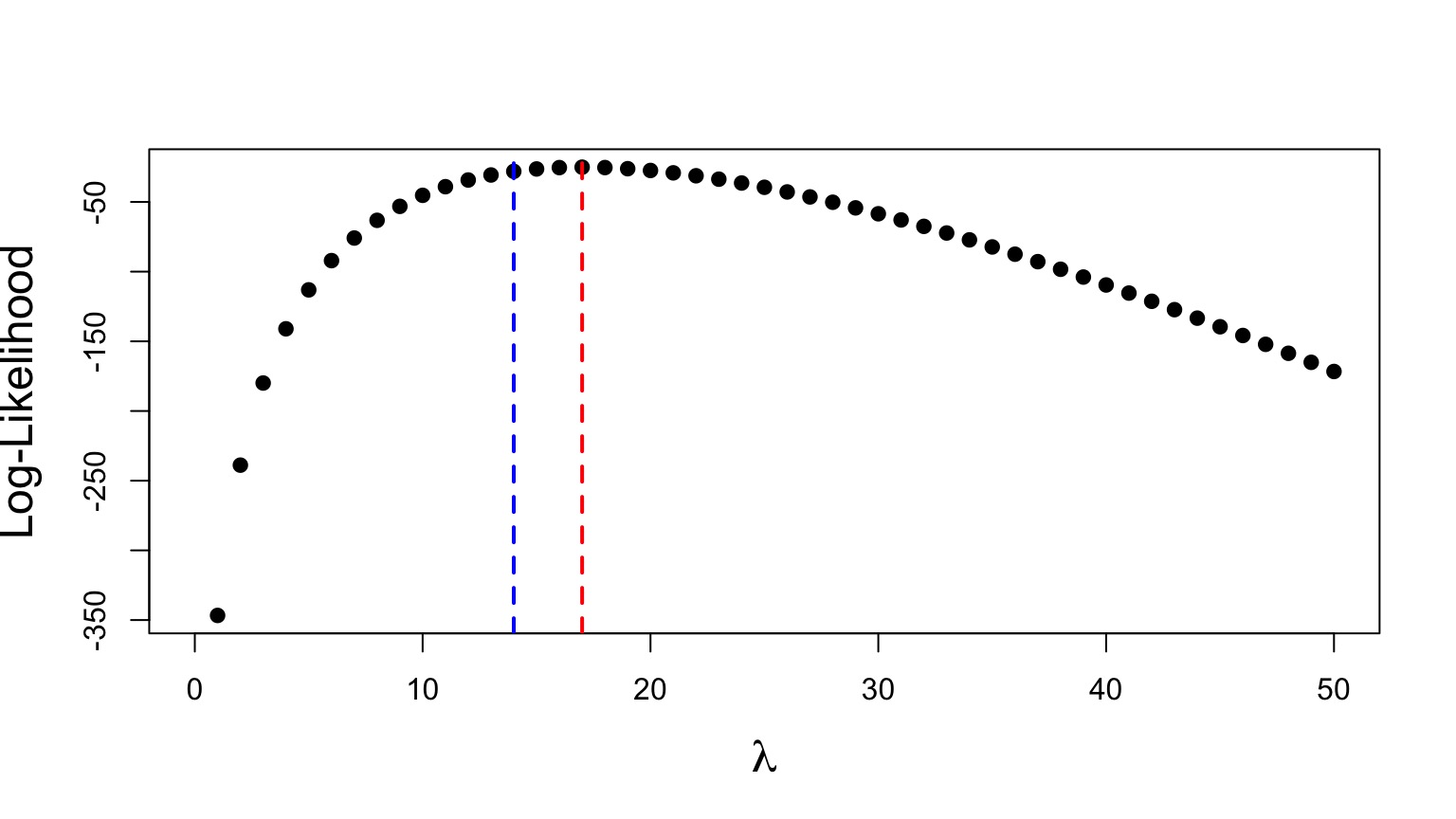
\[G = \frac{L(\lambda = 14 | D)}{L(\lambda = 17 | D)}\]
=0.0494634
Likelihood Ratio Test at Work
 \[D = 2 [Log(L(\lambda = 14 | D)) - Log(L(\lambda = 17 | D))]\] =6.0130449 with 1DF
\[D = 2 [Log(L(\lambda = 14 | D)) - Log(L(\lambda = 17 | D))]\] =6.0130449 with 1DF
p =0.01
Outline
- Review of Likelihood
- Comparing Models with Likelihood
- Linear Regression with Likelihood
Putting Likelihood Into Practice with Pufferfish
- Pufferfish are toxic/harmful to predators
- Batesian mimics gain protection from predation
- Evolved response to appearance?
- Researchers tested with mimics varying in toxic pufferfish resemblance
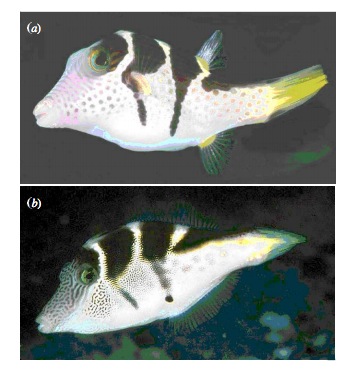
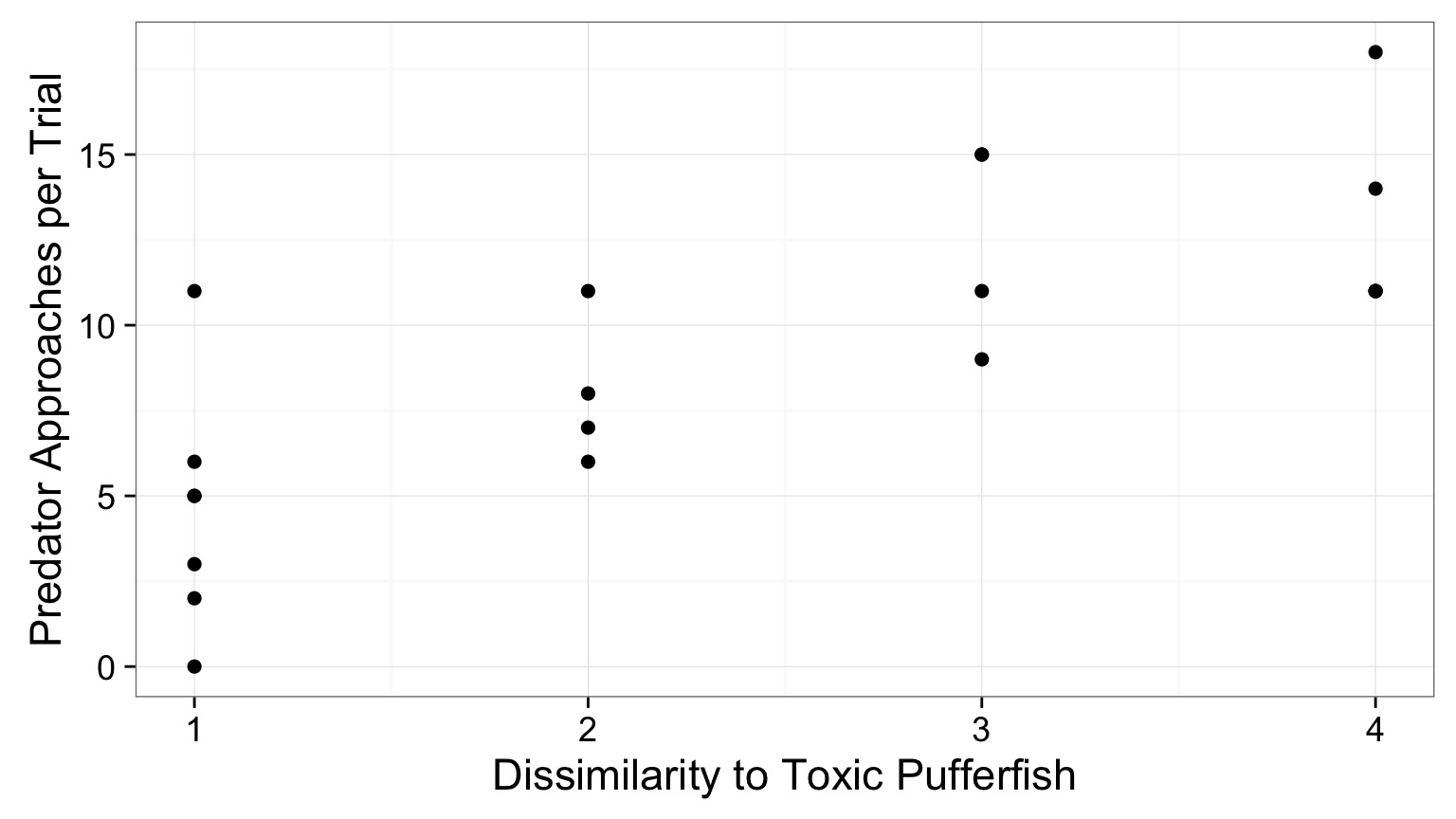
Does Resembling a Pufferfish Reduce Predator Visits?
The Steps of Statistical Modeling
- What is your question?
- What model of the world matches your question?
- Build a test
- Evaluate test assumptions
- Evaluate test results
- Visualize
The World of Pufferfish
Data Generating Process:
\[Visits \sim Resemblance\]Error Generating Process:
Quantiative Model of Process
\[\Large Visits_i = \beta_0 + \beta_1 Resemblance_i + \epsilon_i\]
\[\Large \epsilon_i \sim N(0, \sigma)\]
Likelihood Function for Linear Regression
\(\large L(\theta | D) = \prod_{i=1}^n p(y_i\; | \; x_i;\ \beta_0, \beta_1, \sigma)\)
Likelihood Function for Linear Regression
\[L(\theta_j | Data) = \prod_{i=1}^n \mathcal{N}(Visits_i\; |\; \beta_{0j} + \beta_{1j} Resemblance_i, \sigma_j)\]
where \(\beta_{0j}, \beta_{1j}, \sigma_j\) are elements of \(\theta_j\)
Fit Your Model!
library(bbmle)
puffer_mle <- mle2(predators ~ dnorm(b0 + b1*resemblance, sd = resid_sd),
data=puffer,
start=list(b0=1, b1=1, resid_sd = 2))The Same Diagnostics
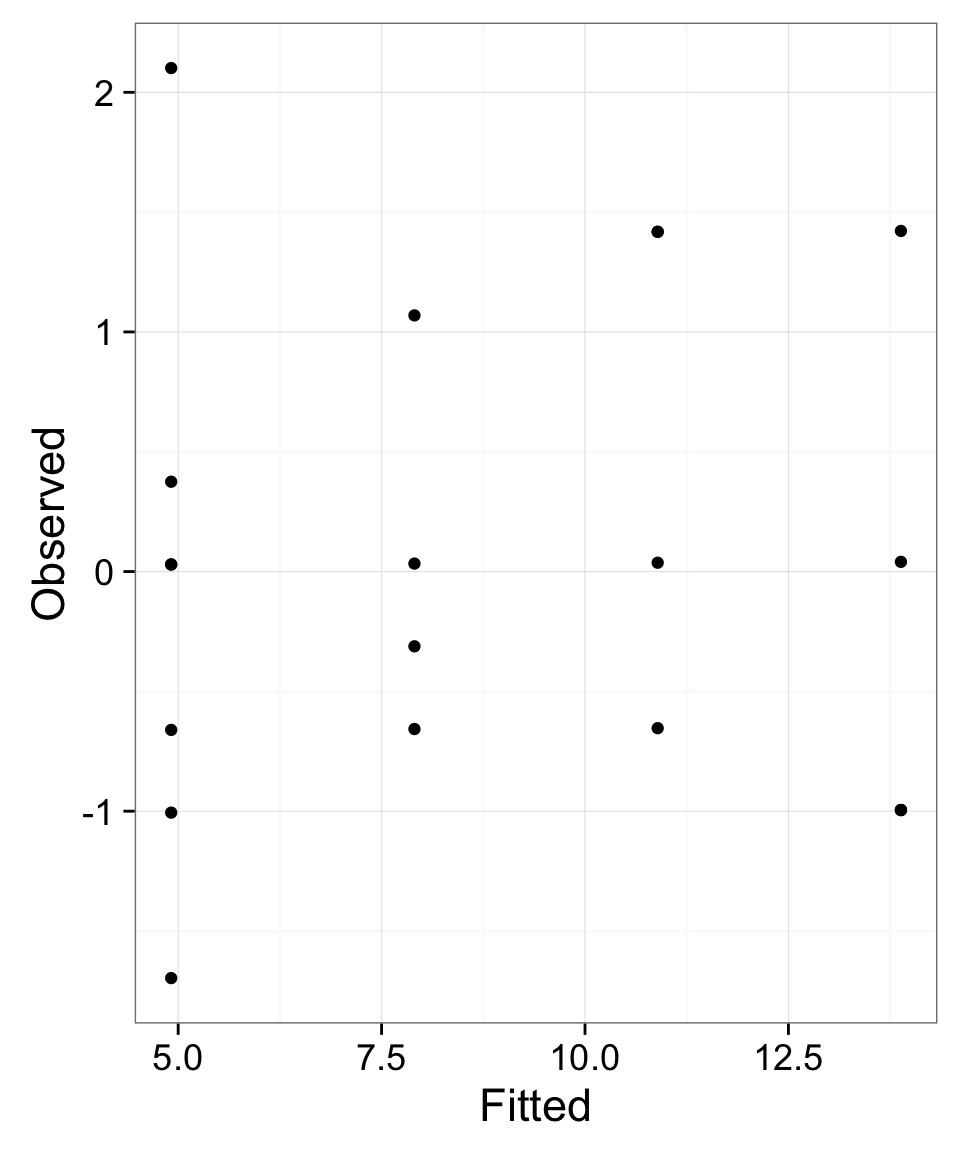
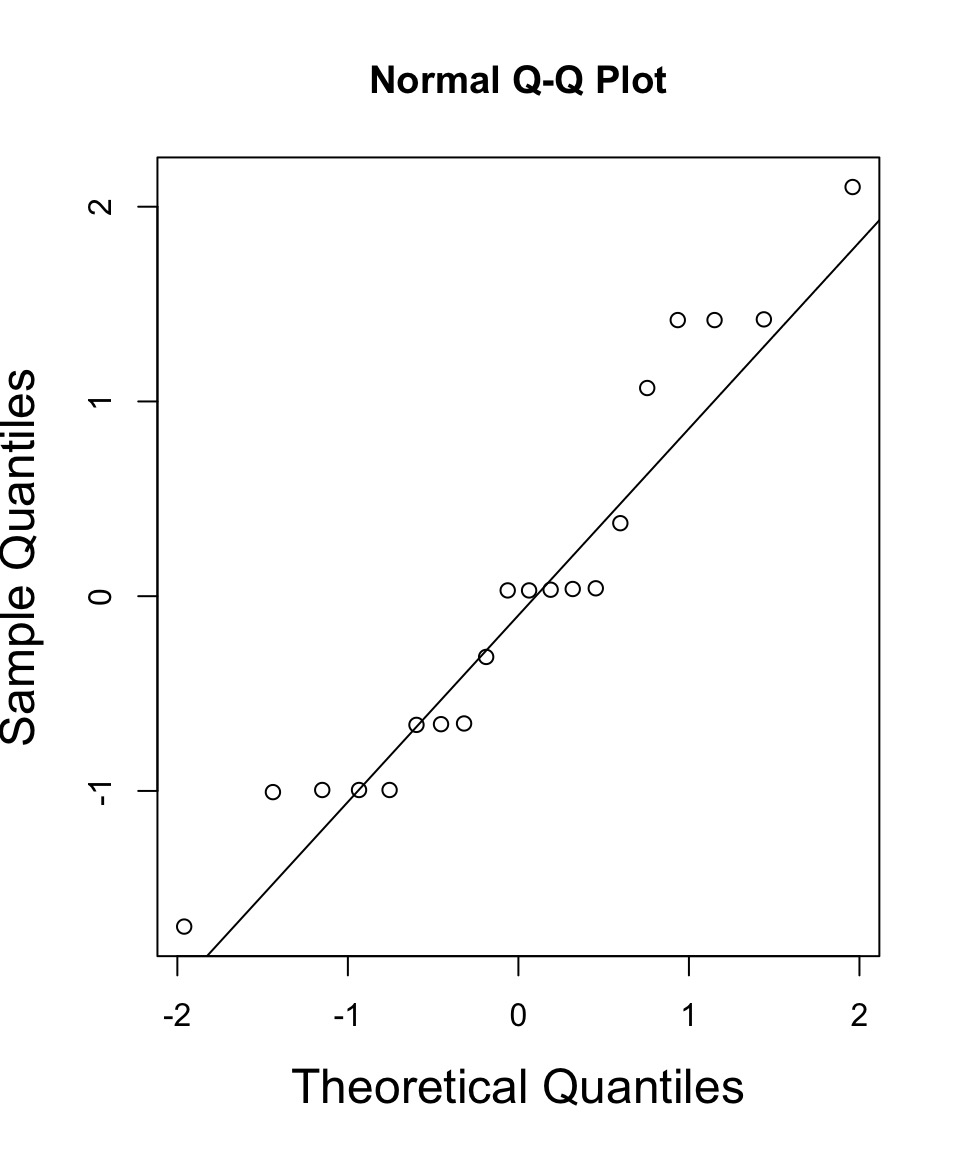
But - What do the Likelihood Profiles Look Like?
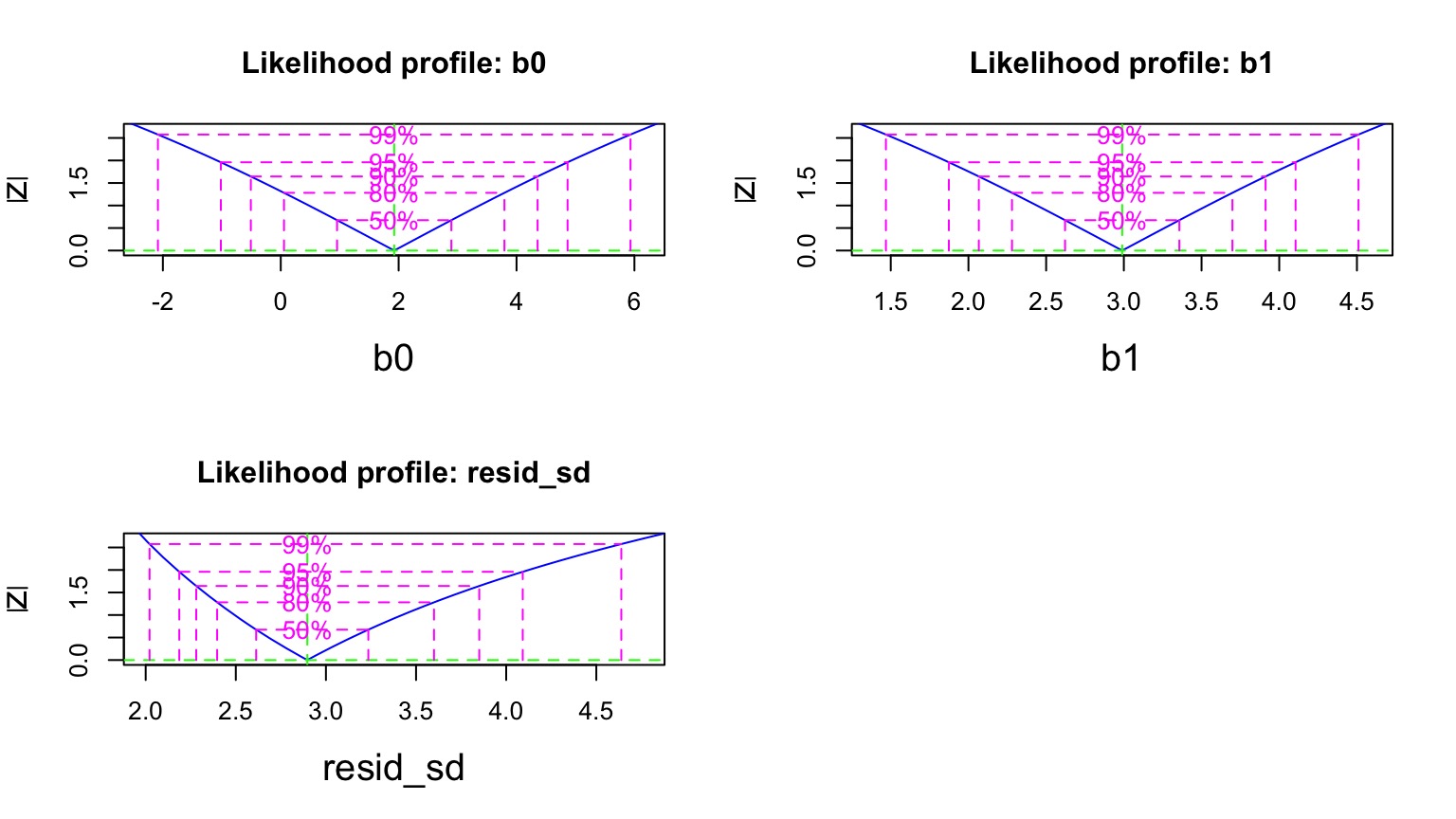
Are these nice symmetric slices?
Evaluate Coefficients
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| b0 | 1.924604 | 1.4291143 | 1.346711 | 0.1780732 |
| b1 | 2.989502 | 0.5420939 | 5.514730 | 0.0000000 |
| resid_sd | 2.896527 | 0.4579823 | 6.324540 | 0.0000000 |
Test Statistic is a Wald Z-Test Assuming a well behaved quadratic Confidence Interval
Confidence Intervals
Quadratic Assumption
| 2.5 % | 97.5 % | |
|---|---|---|
| b0 | -1.016771 | 4.866158 |
| b1 | 1.873731 | 4.105253 |
| resid_sd | 2.187663 | 4.092085 |
Spline Fit to Likelihood Surface
| 2.5 % | 97.5 % | |
|---|---|---|
| b0 | -1.016771 | 4.866158 |
| b1 | 1.873731 | 4.105253 |
| resid_sd | 2.187663 | 4.092085 |
To test the model, need an alternate hypothesis
puffer_null_mle <- mle2(predators ~ dnorm(b0, sd = resid_sd),
data=puffer,
start=list(b0=14, resid_sd = 10))Put it to the Likelihood Ratio Test!
Likelihood Ratio Tests
Model 1: puffer_mle, predators~dnorm(b0+b1*resemblance,sd=resid_sd)
Model 2: puffer_null_mle, predators~dnorm(b0,sd=resid_sd)
Tot Df Deviance Chisq Df Pr(>Chisq)
1 3 99.298
2 2 117.788 18.49 1 1.708e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Compare to Linear Regression
Likelihood:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| b0 | 1.924604 | 1.4291143 | 1.346711 | 0.1780732 |
| b1 | 2.989502 | 0.5420939 | 5.514730 | 0.0000000 |
| resid_sd | 2.896527 | 0.4579823 | 6.324540 | 0.0000000 |
Least Squares
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 1.924694 | 1.5064163 | 1.277664 | 0.2176012 |
| resemblance | 2.989492 | 0.5714163 | 5.231724 | 0.0000564 |
Compare to Linear Regression: F and Chisq
Likelihood:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| b0 | 1.924604 | 1.4291143 | 1.346711 | 0.1780732 |
| b1 | 2.989502 | 0.5420939 | 5.514730 | 0.0000000 |
| resid_sd | 2.896527 | 0.4579823 | 6.324540 | 0.0000000 |
Least Squares
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| resemblance | 1 | 255.1532 | 255.153152 | 27.37094 | 5.64e-05 |
| Residuals | 18 | 167.7968 | 9.322047 | NA | NA |