Quantifying Goodness of Fit: the \[\chi^2\]
Number of Observations in Categories
Consider the following data generating process:
- We have a number of categories
- We expect some number of observations in each category
Then add this error generating process:
> - Small random errors generating variation in observed values
> - This error is normal
Do our observed values fit our expectations?
- \(H_0\): Observations = Expectations
- We are testing goodness of fit!
- If there is no difference, deviations should be normally distributed noise
- Differences can be positive or negtive - so we square them
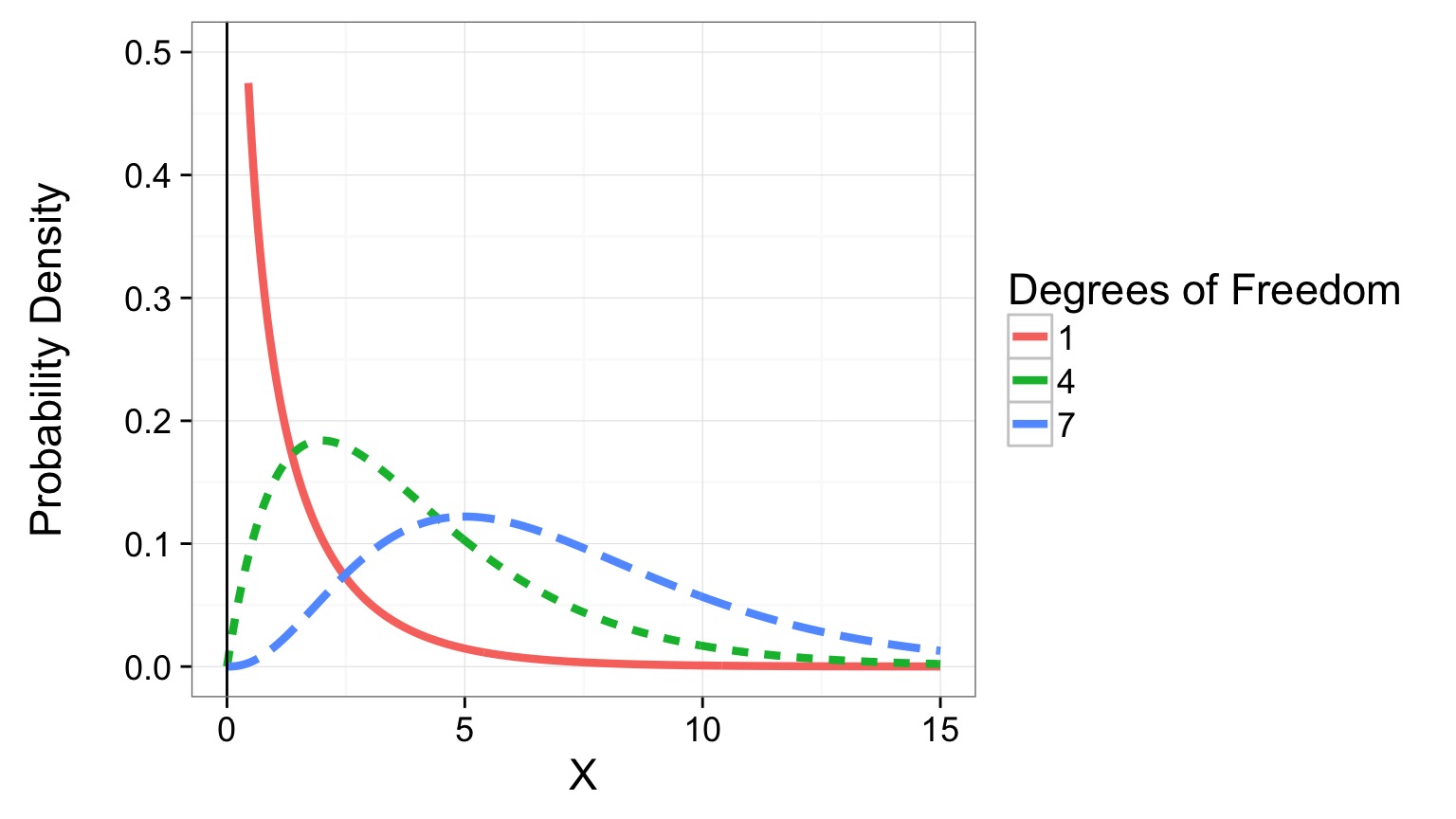
- The square of a normal distribution is the χ2 distribution!
- The χ2 is defined by degrees of freedom = n-1!
The \(\chi^2\) Distribution
\[\chi^2 = \sum\frac{\displaystyle(O_i-E_i)^2}{E_i}\]
Birth Days
 {width = 80%}
{width = 80%}
Are births evenly spread across the week?
Birth Days
Day.of.the.Week Births
1 Sunday 33
2 Monday 41
3 Tuesday 63
4 Wednesday 63
5 Thursday 47
6 Friday 56
7 Saturday 47Even Expectations
Day.of.the.Week Births Expectation
1 Sunday 33 50
2 Monday 41 50
3 Tuesday 63 50
4 Wednesday 63 50
5 Thursday 47 50
6 Friday 56 50
7 Saturday 47 50
\(\chi^2\) = 15.24 with 6 DF
p = 0.01847
Assumptions of \(\chi^2\) test
Given that the goal is to detect deviations from expectations given normal error, this test has a few assumptions:
- No expected values less that 1
- 80% of the expected values must be >5
If you violate assumptions:
- Combine categories or
- Use a different test (e.g., Fisher’s Exact).