Probability and Frequentist Hypothesis Testing

https://xkcd.com/882/

Quiz!

http://tinyurl.com/hyp-pre-quiz

Etherpad for this week

https://etherpad.wikimedia.org/p/607-hypotheses

Roadmap

Basic Probability Review
The normal distribution & P-Values
Hypothesis testing

Probability Distributions & What they can Do for You!

So far, we’ve been slinging around normal distribution terminology casually. Let’s formalize it, and make it useful for hypothesis testing!

Probability!

Probability - The fraction of observations of an event given multiple repeated independent observations.

Probability of Eating

Let’s say you’ve offered 50 budworms a leaf to eat. 45 eat.

\(P(eats) = \frac{45}{50} = 0.9\)

Now you offer 50 others a leaf. 10 eat.

\(P(eats) = \frac{10}{50} = 0.2\)

Probability of Exclusive Feeding Events

We offered our budworms two different leaves
20 eat the first, 5 eat the second.
What is the probability of eating one or the other?

P(A or B) = P(A) + P(B)

P(eats) = \(\frac{20}{50} + \frac{5}{50} = 0.5\)

Probability of Joint Events

We offer our budworms a leaf. 45 eat it. Then we offern all of them another leaf. 20 eat it. What is the probability of eating one and the other?

P(A and B) = P(A)P(B)

P(eats twice) = \(\frac{45}{50} * \frac{20}{45}\)
= \(\frac{20}{50}\) = 0.4

JOINT PROBABILITY

Distributions!

(when a point probabilty just ain’t enough)

Frequency Distributions Make Intuitive Sense

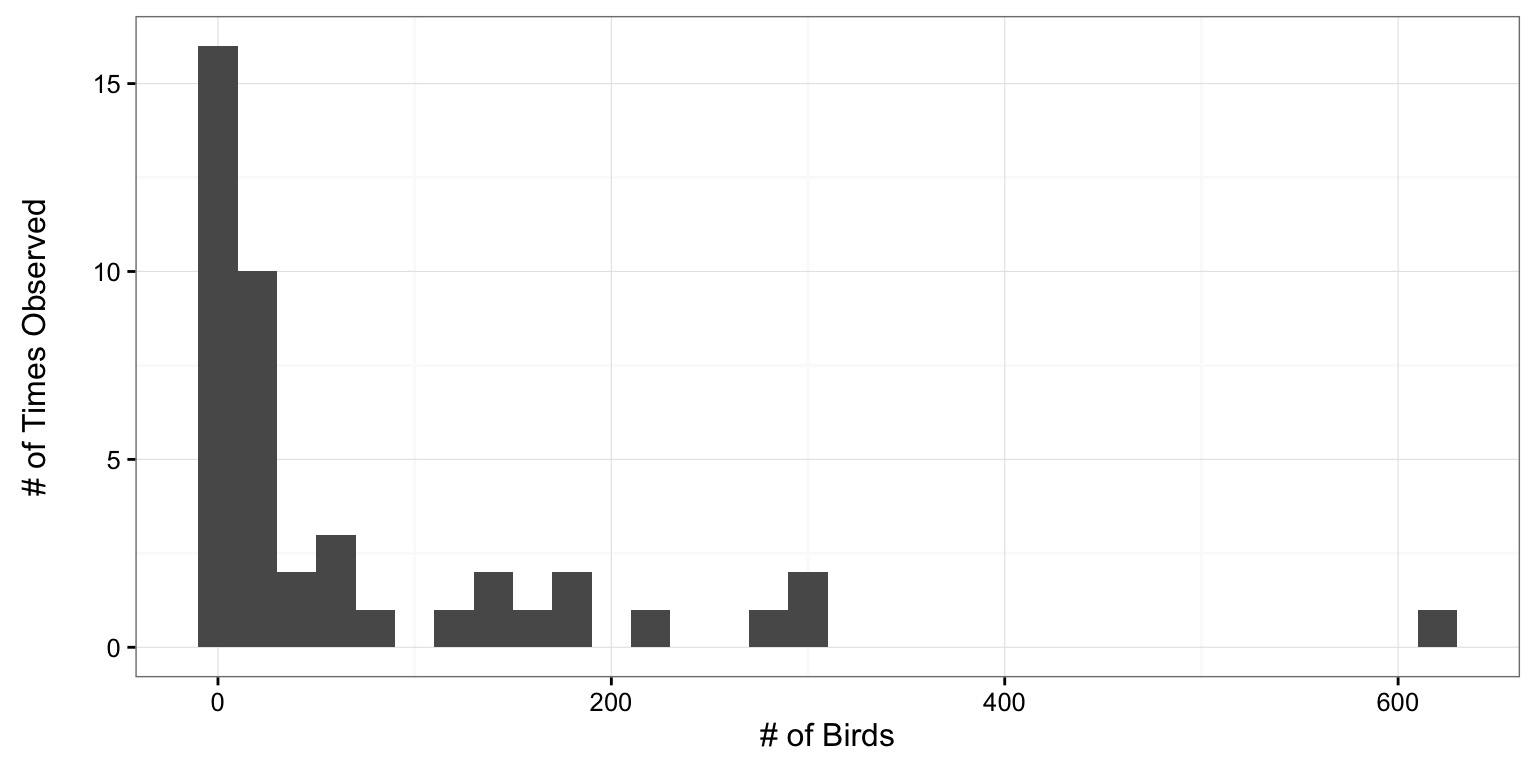
Frequencies Can be Turned Into Probabilities

Just divide by total # of observations

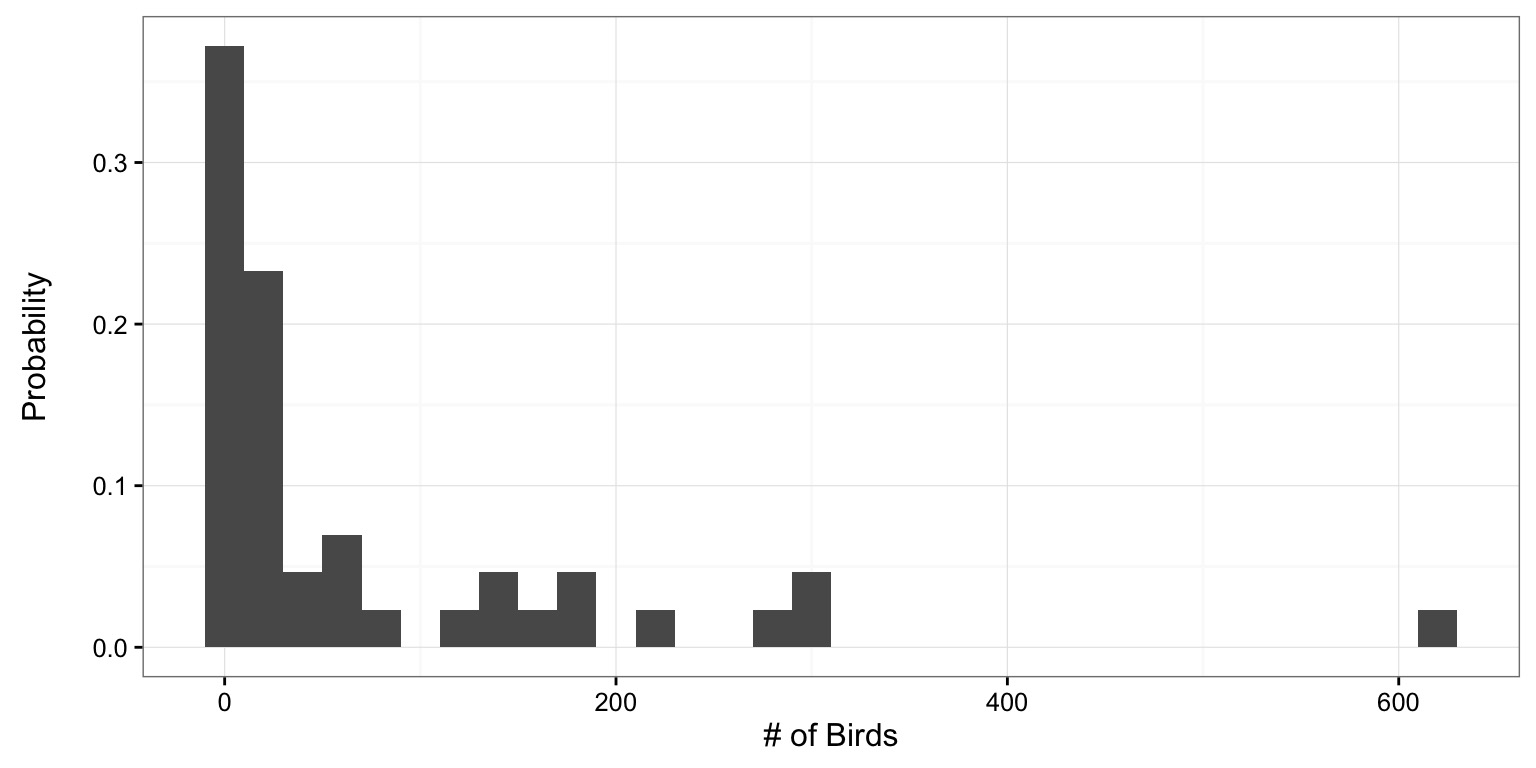
But - we have binned observations…

Probabilities of Individual Observations

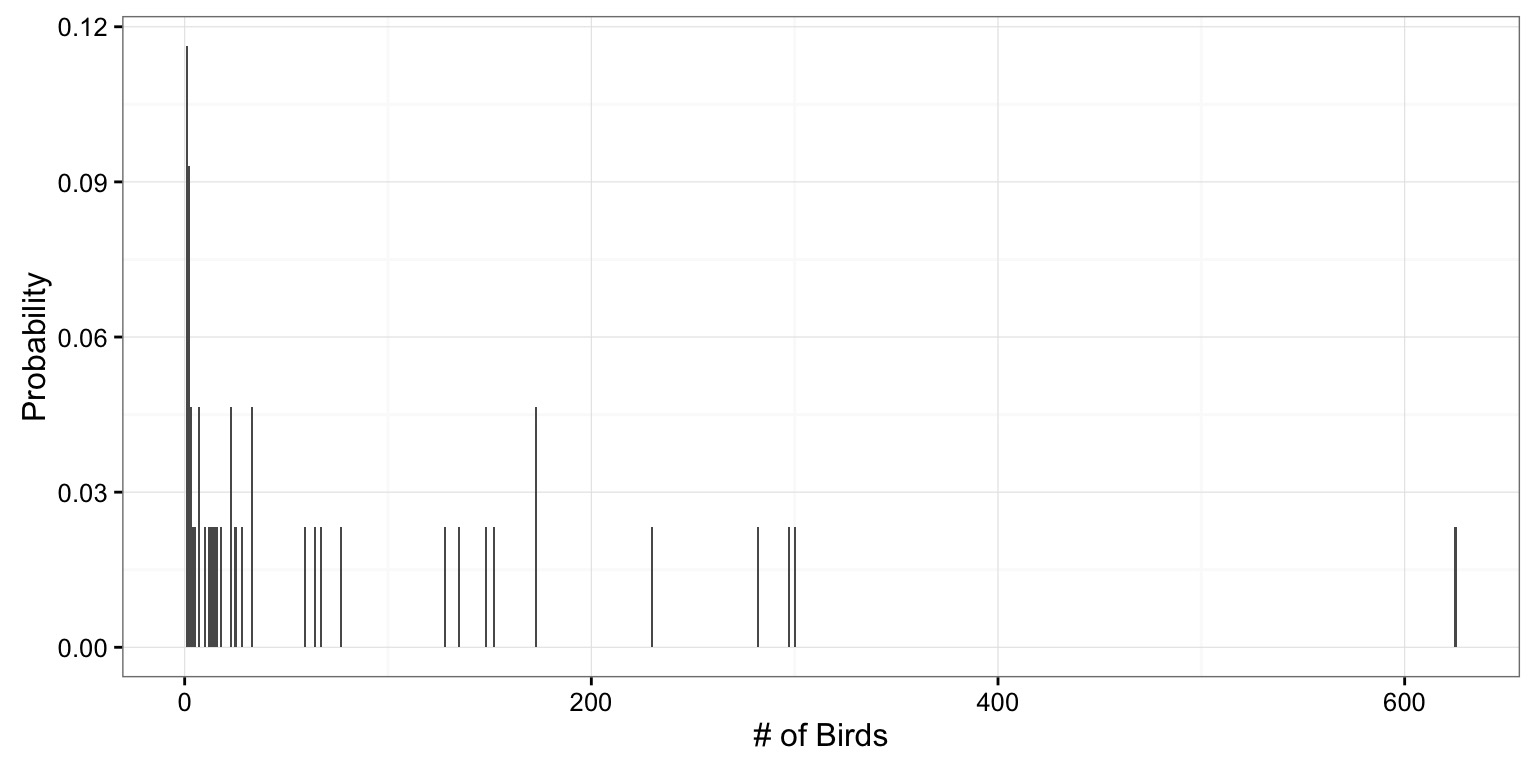
Tradeoff: Bins or we need to find something that fills gaps

Continuous Probability Distributions

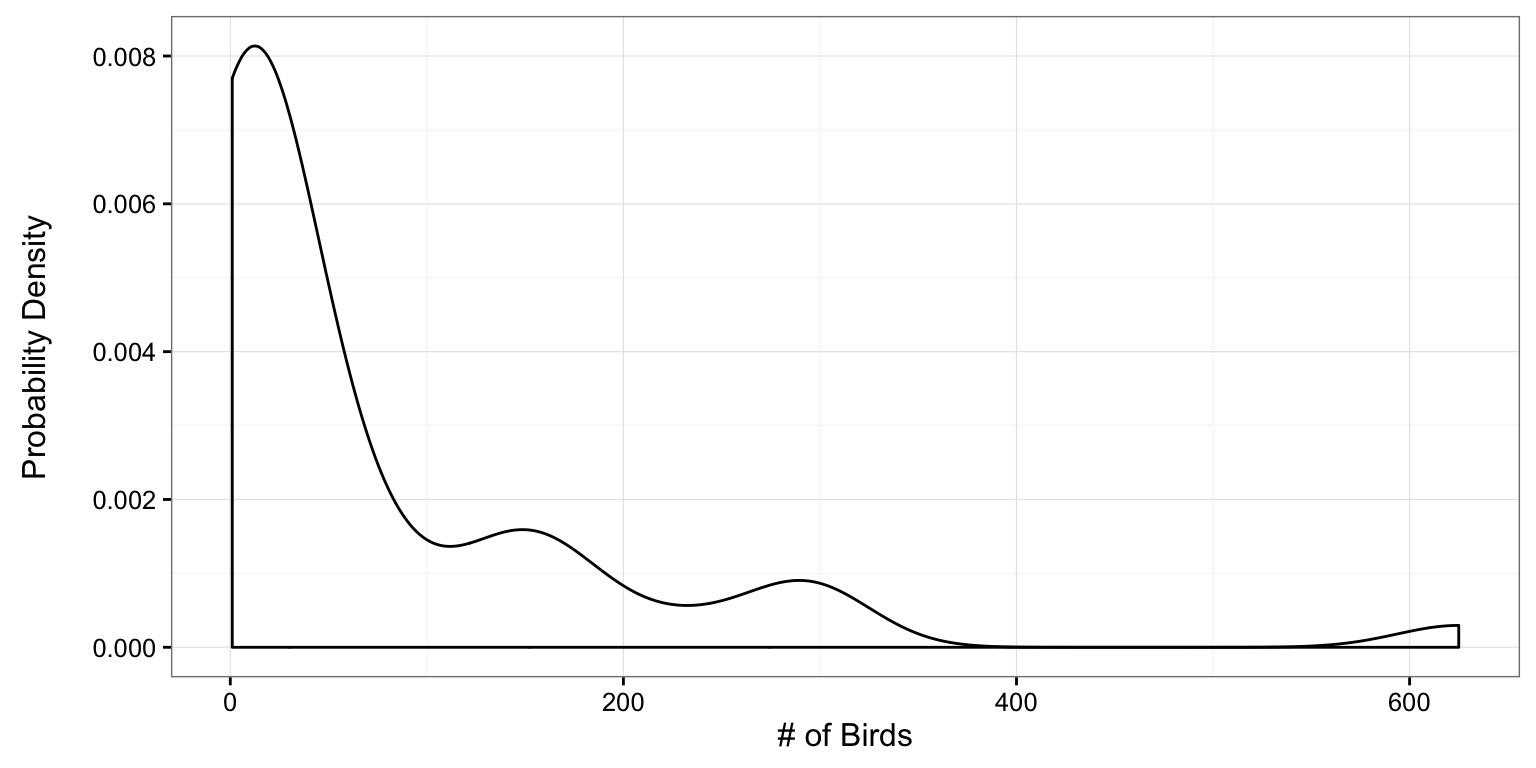
Any individual observation has a probability density.

Probability of a Range of Values

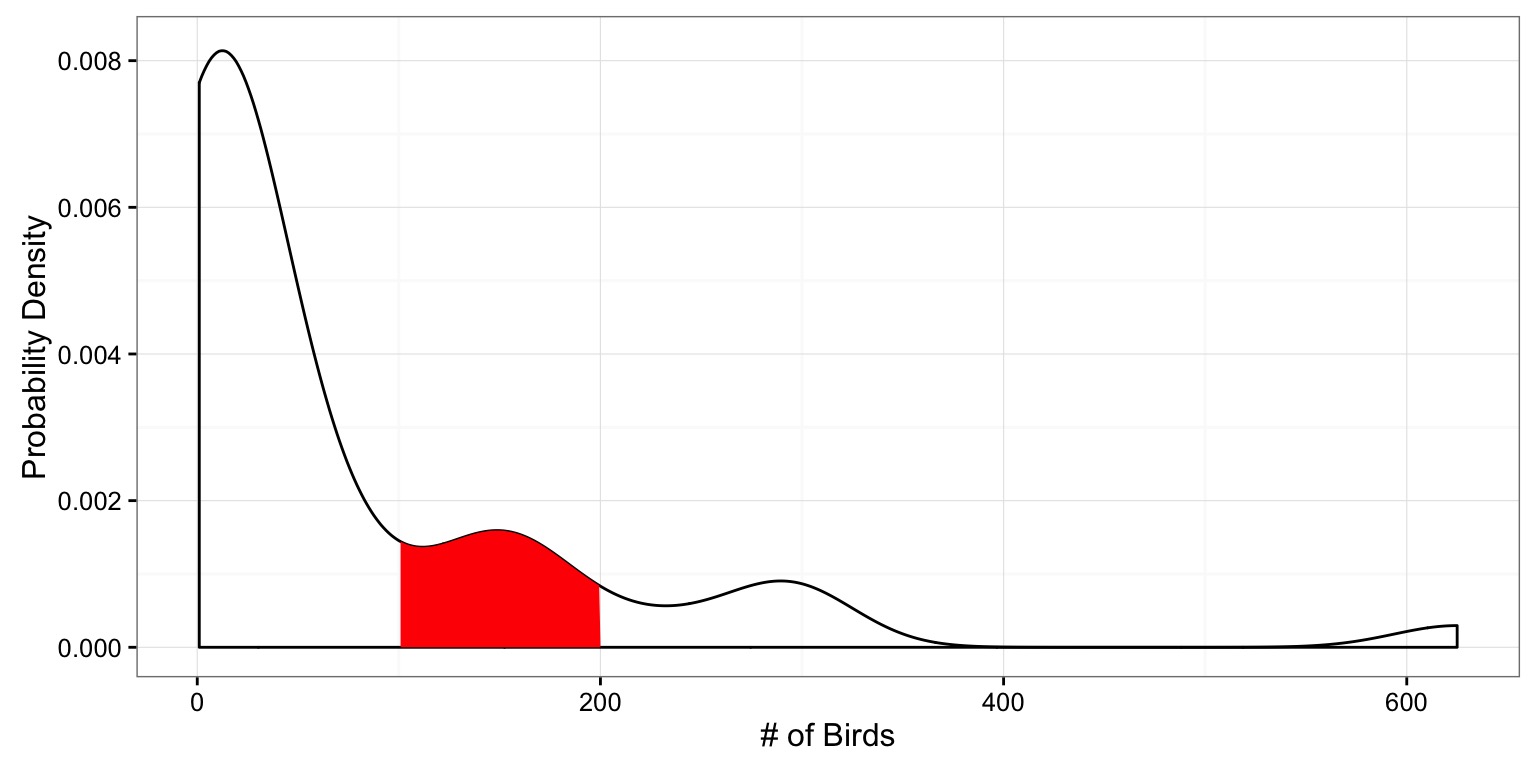
What is the probability of a value between 100 and 200?

Probability of a range of values

We obtain probabilities of observations between a range of values by integrating the distribution over selected values.

Probability as Integral Under the Curve

\(\int_{i=100}^{200}{P(a=i)}\)

Roadmap

Basic Probability Review
The normal distribution & P-Values
Hypothesis testing

The Normal Distribution

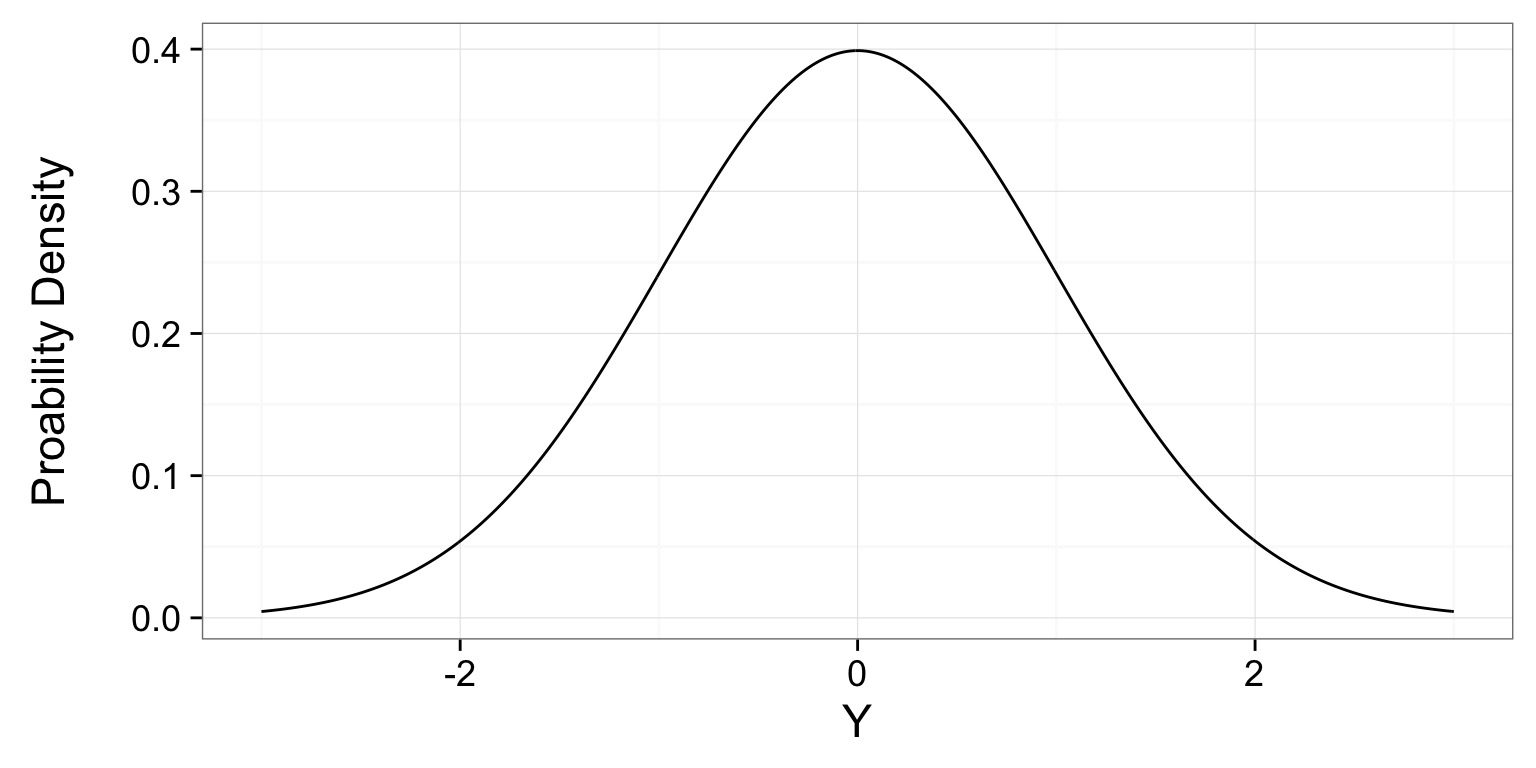
A single mean data generating process
Many sources of variation (error) with equal probability
Low probability of ending up in tails, high in middle

67% of Values within 1 SD

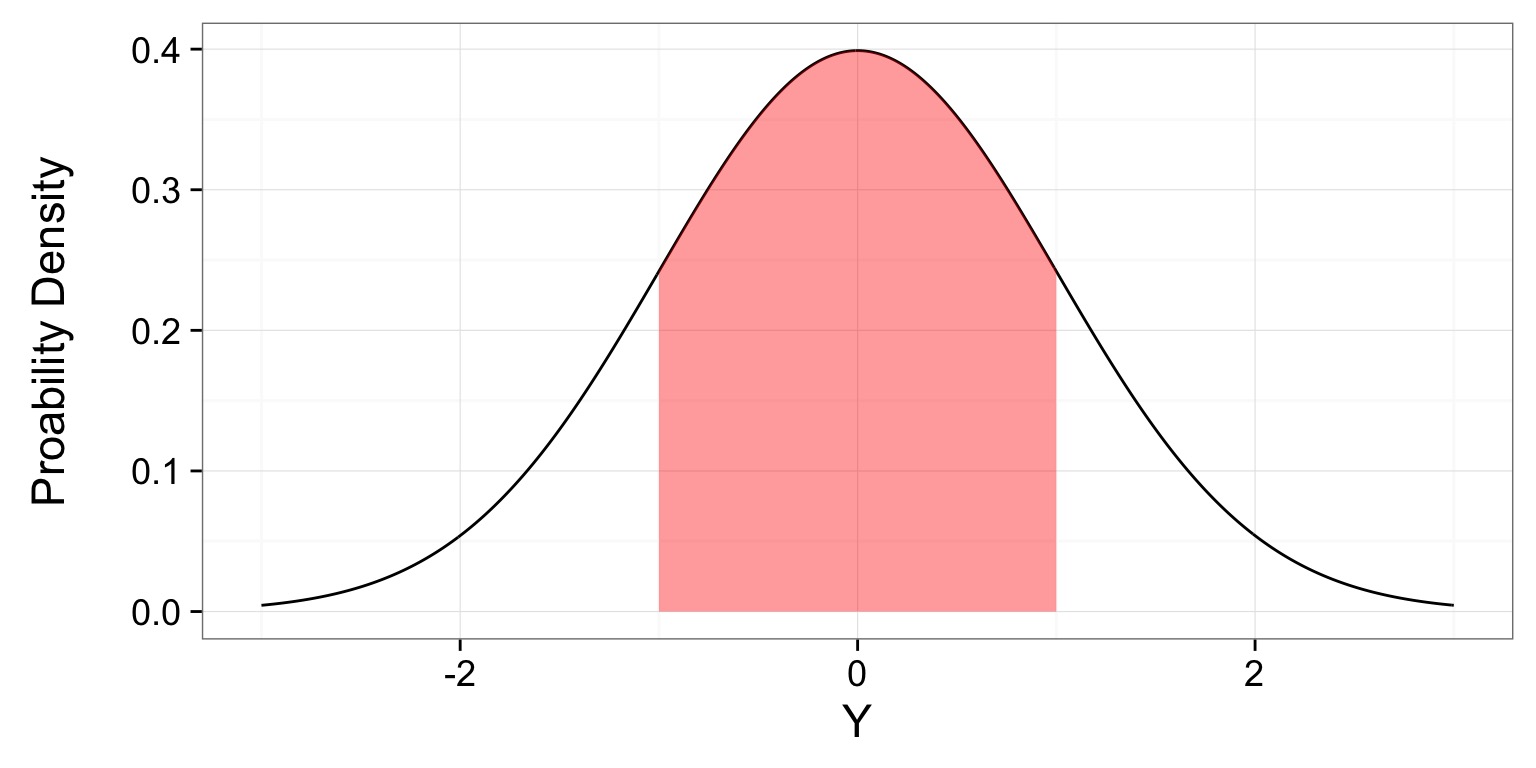
If we summed up the probability densities under the curve, it would be 0.67

95% of Values within 2 (1.96) SD

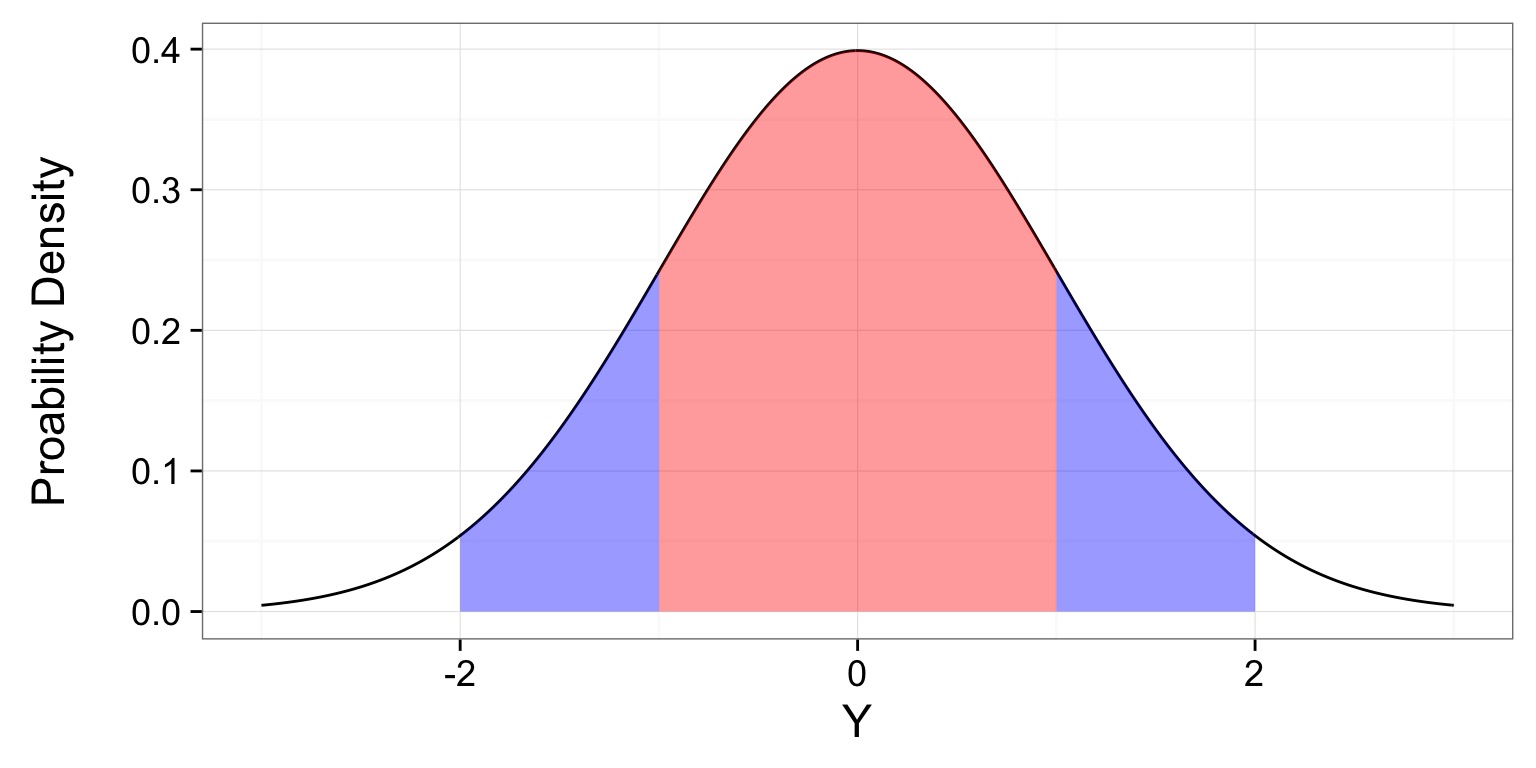
If we summed up the probability densities under the curve, it would be 0.95

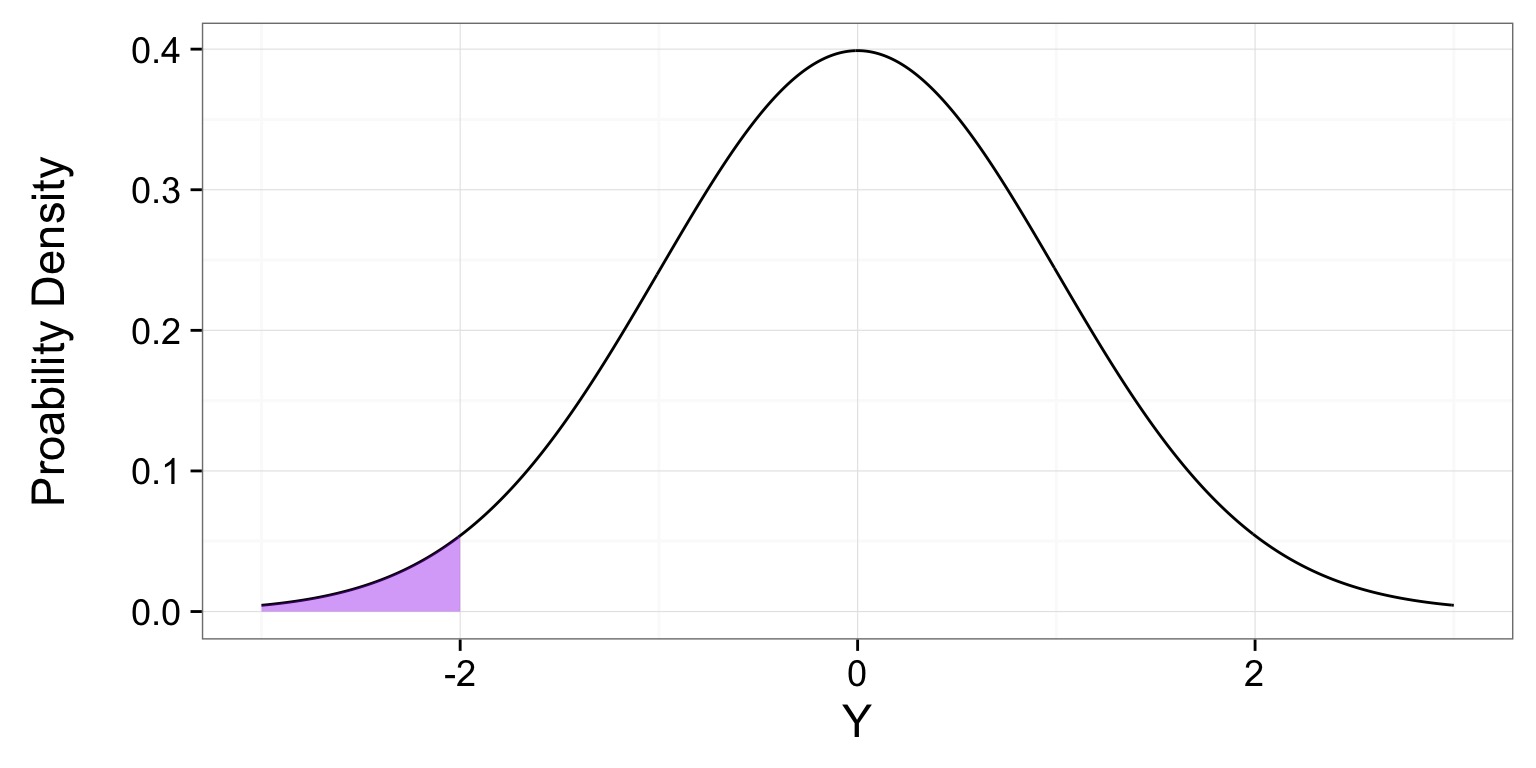
The Probability of a Value or More Extreme Value

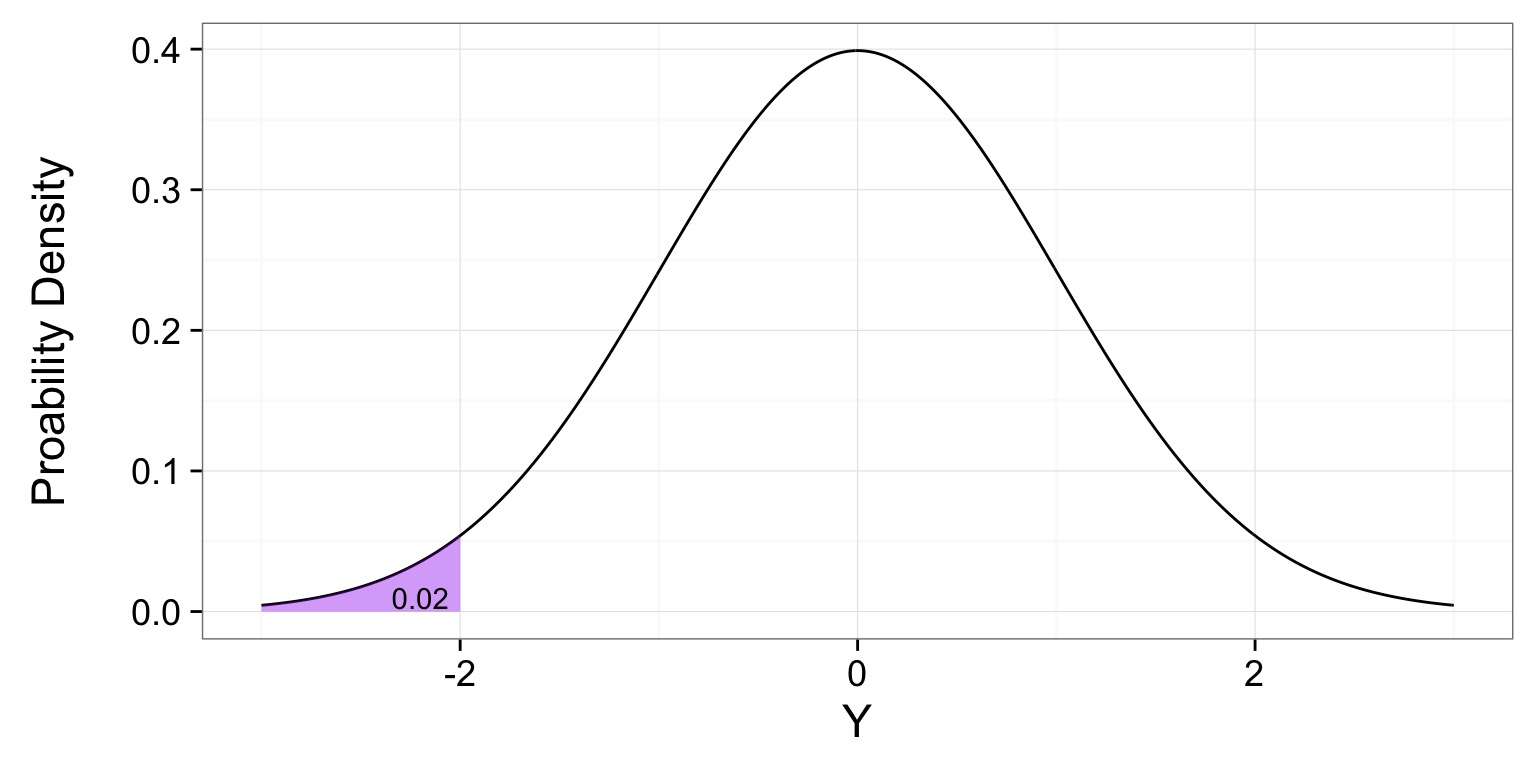
This is a p-value

P-Values

The probability of observing a value or more extreme value in a distribution.

The Probability of a Value or More Extreme Value

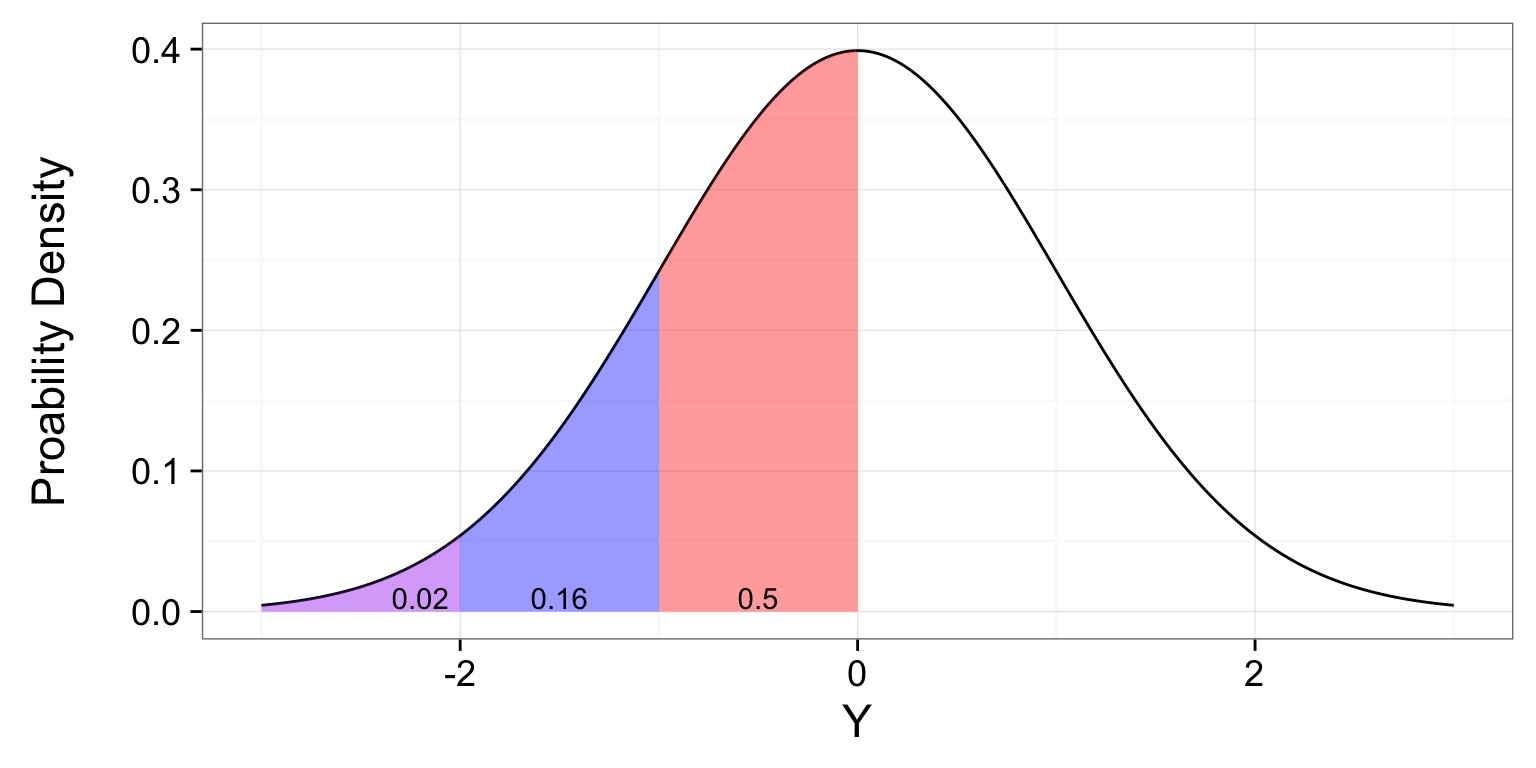
The Cummulative Distribution/Quantile Function

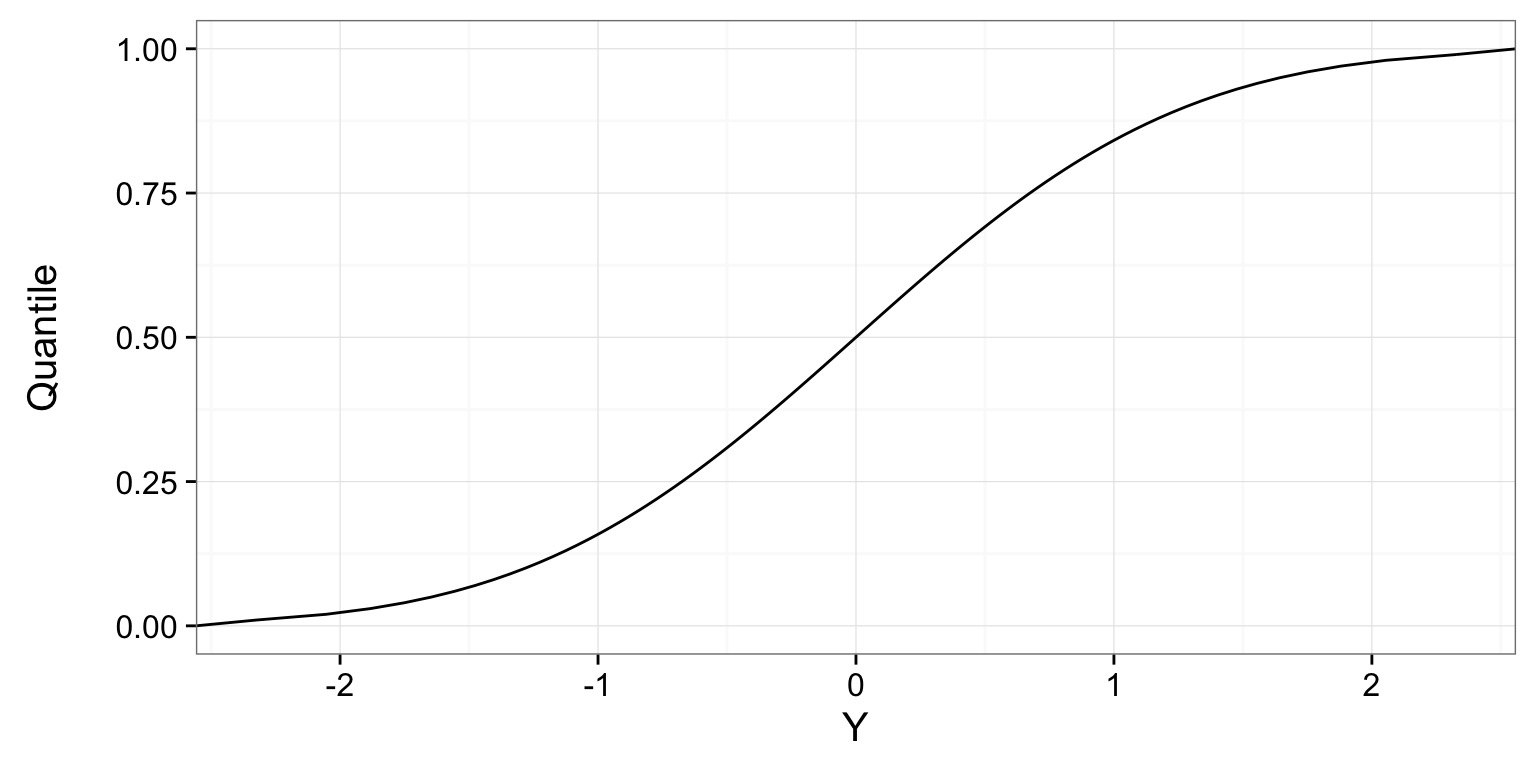
How p-value changes with different values of a distribution

Roadmap

Basic Probability Review
The normal distribution & P-Values
Hypothesis testing

Hypothesis Testing

Inductive v. Deductive Reasoning

Deductive Inference: A larger theory is used to devise many small tests.

Inductive Inference: Small pieces of evidence are used to shape a larger theory and degree of belief.

Deriving Truth from Data

Frequentist Inference: Correct conclusion drawn from repeated experiments
- Uses p-values and CIs as inferential engine
Likelihoodist Inference: Evaluate the weight of evidence for different hypotheses
- Derivative of frequentist mode of thinking
- Uses model comparison (sometimes with p-values…)
Bayesian Inference: Probability of belief that is constantly updated
- Uses explicit statements of probability and degree of belief for inferences

Primary Mode of Frequentist Inference

Null Hypothesis Tests: Falsify a null hypothesis : Evaluate weight of evidence

Null Hypothesis Tests & Popper

Falsification of hypotheses is key!

A theory should be considered scientific if, and only if, it is falsifiable.

Deductive Reasoning and Null Hypothesis Tests

A null hypothesis is a default condition that we can attempt to falsify.

Common Uses of Null Hypothesis Tests

Ho: Two groups are the same
Ho: An estimated parameter is not different from 0
Ho: The slopes of two lines are the same
Etc…

So, what conclusions can we draw if we reject the null?

Null Distributions

Null hypotheses are associated with null statistical distributions.
For example, if Ho states that a value is normally distributed, but not different from 0, the null distribtion is centered on 0 with some standard deviation.
We then assess whether an observed value or more extreme value than our observation is likely.

Null Distributions

R.A. Fisher and The P-Value For Null Hypotheses

P-value: The Probability of making an observation or more extreme observation given that the null hypothesis is true.

Evaluation of a Test Statistic

We use our data to calculate a test statistic that maps to a value of the null distribution.

We can then calculate the probability of observing our data, or of observing data even more extreme, given that the null hypothesis is true.

\(P(X \leq Data | H_{0})\)

Evaluation of a Test Statistic

Let’s say we know the distribution of chest hair lengths on Welsh Corgis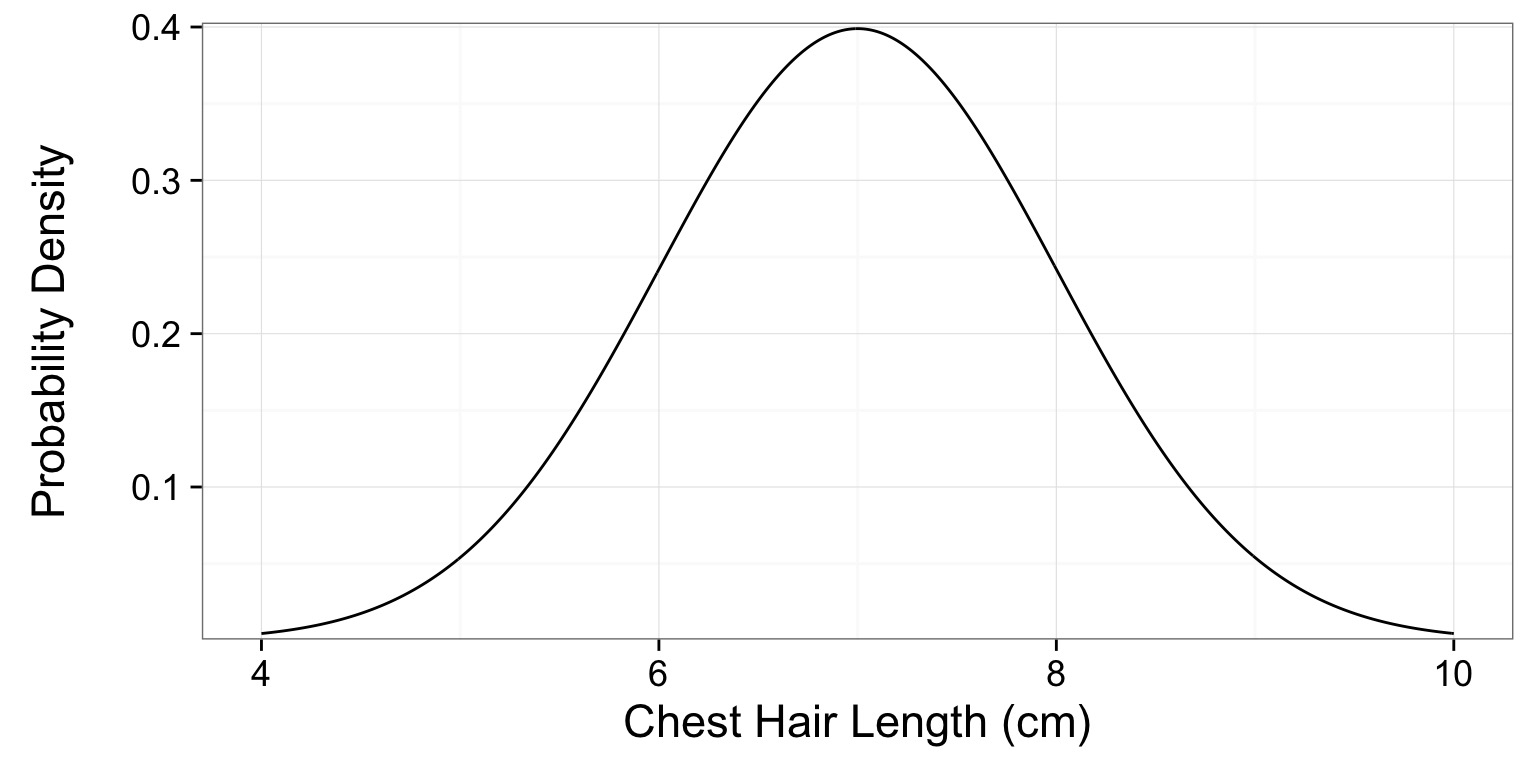

A short-haired Corgi

You have a Corgi with a chest hair that is 5 cm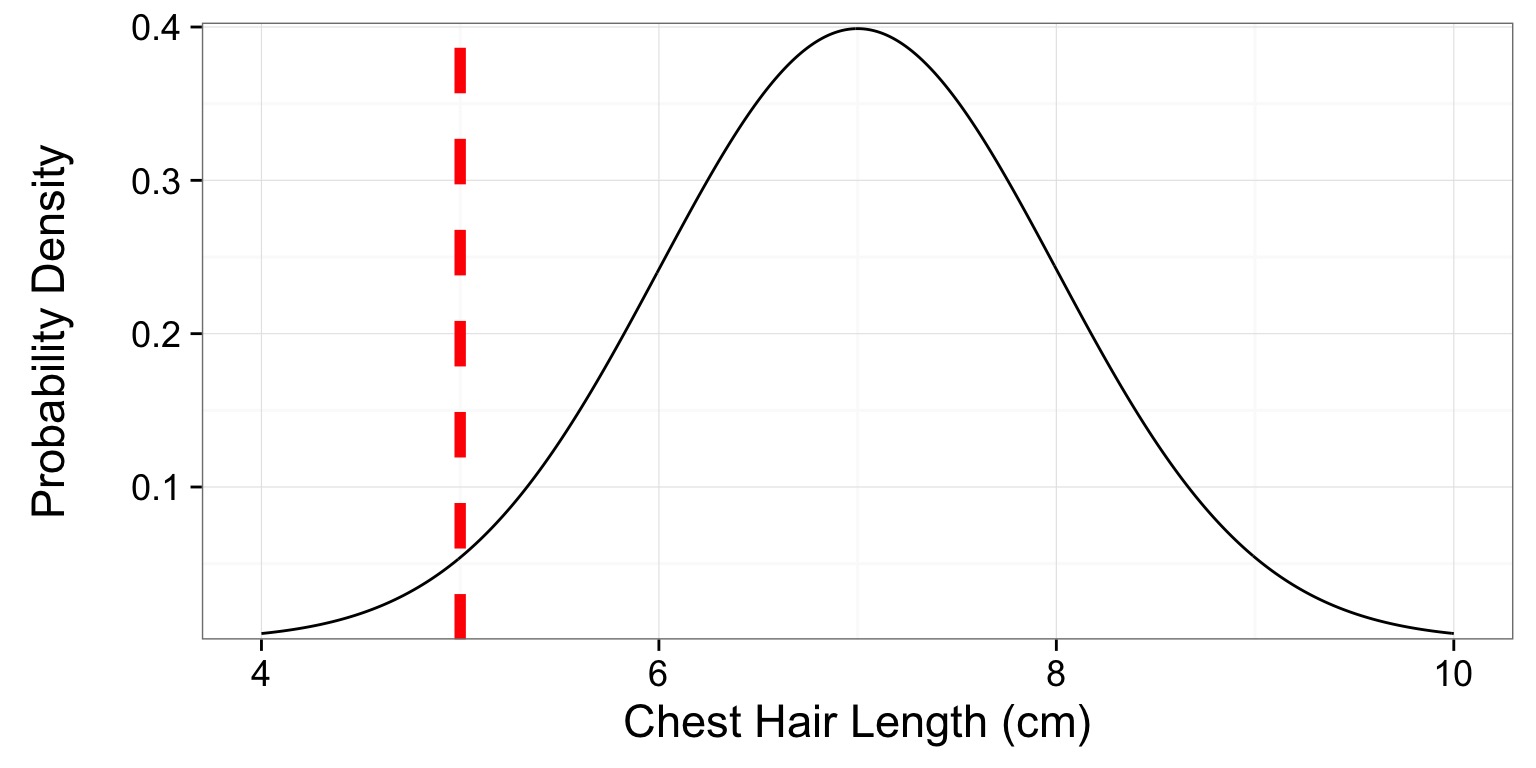

A Corgi’s P

What is the probability of this or a shorter-haired Corgi?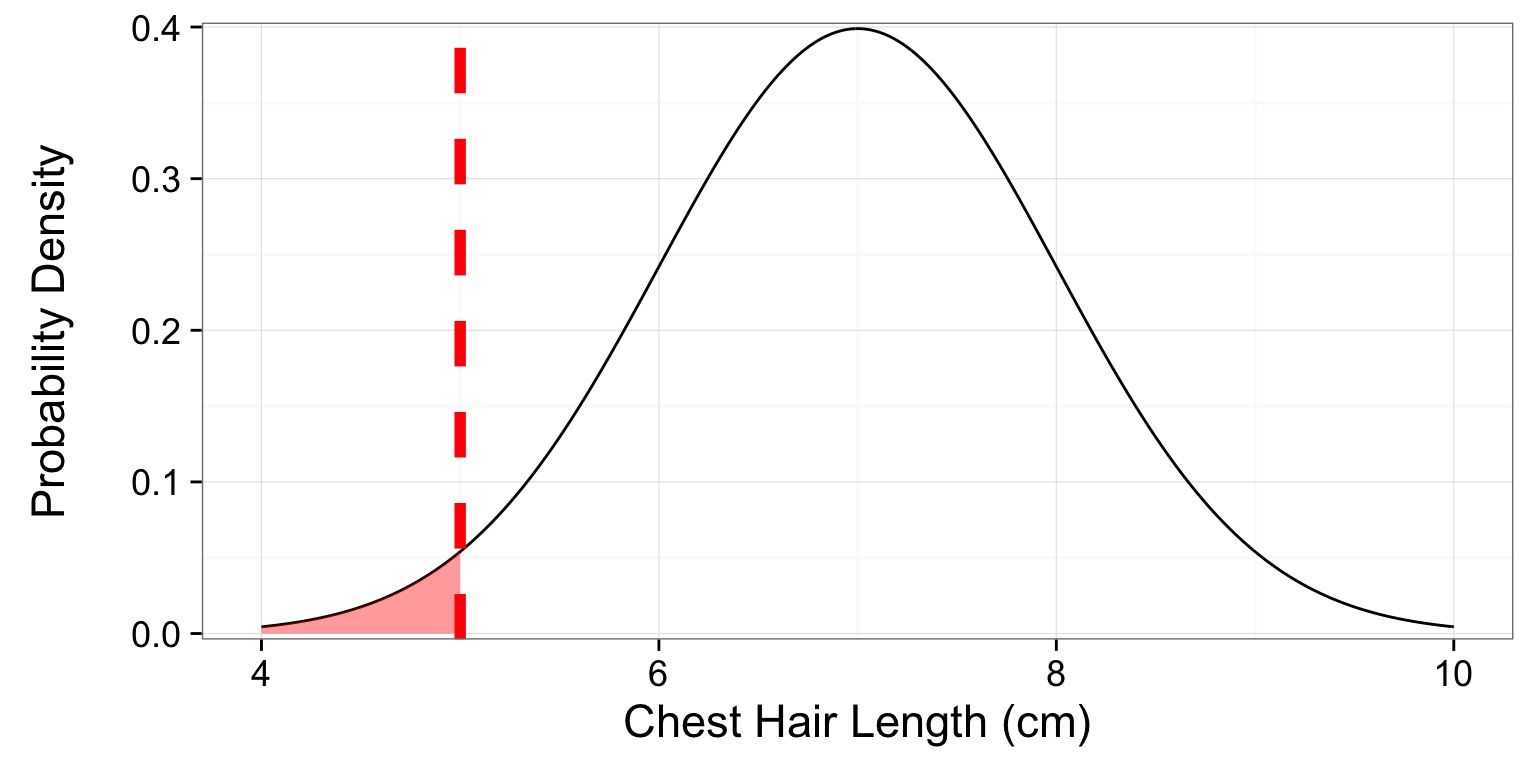

p = 0.0228
Note - this is a one-tailed test!

1-Tailed v. 2-Tailed Tests

1-Tailed Test: We are explicit about whether Ha implies that our sample is greater than or less than our null value.

\(P(X \leq Data | H_{0})\) (1-tailed)

2-Tailed Test: We are make no assumption about the sign or direction of our alternative hypotheses.

\(P(X \leq Data | H_{0}) + P(X \geq Data | H_{0})\) (2-tailed)

Two-Tailed P Value

p = 2 x 0.0228 = 0.0456

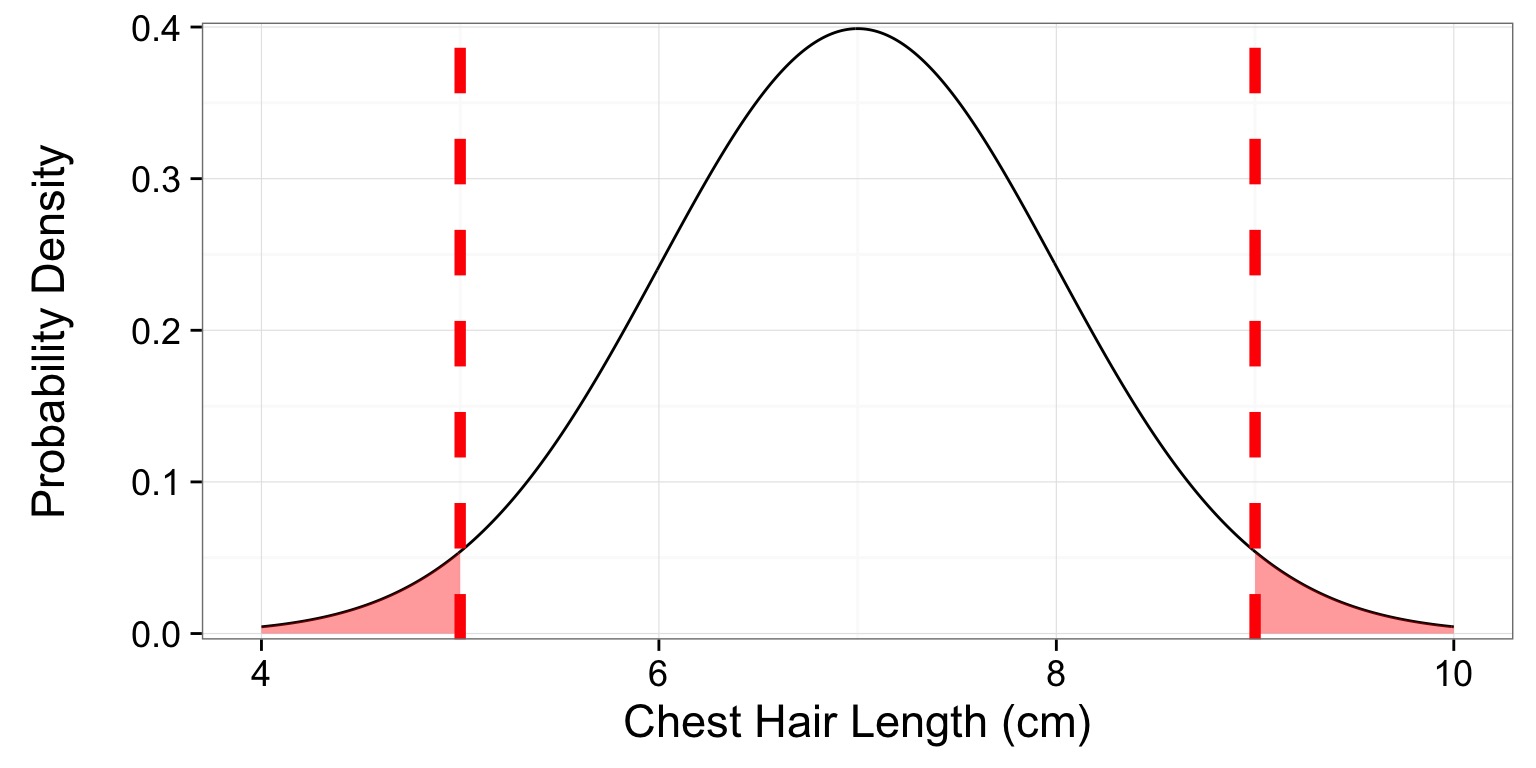
When should you use a 1-Tailed Test?

What does 0.0456 mean?

There is a 4.56% chance of obtaining the observed data, or more extreme data, given that the null hypothesis is true.

If you chose to reject the null, you have a ~ 1 in 22 chance of being wrong.

How comfortable are you with rejecting the null?

Note: rejecting the null ̸= accepting a specific alternative